Možnosti extrapolace digitálního modelu terénu z rastru DMR 5G

Souhrn

Nad územím celé České republiky bylo provedeno letecké laserové snímkování (LiDAR), díky němuž je možné vytvářet rastry digitálního modelu terénu. Tyto podklady mají široké uplatnění v různých odvětvích. Z hlediska potřeb hydrologie je však nedostatkem použité technologie nepřesné, resp. neúplné, vykreslení tvaru koryt, neboť laserové paprsky blízkého infračerveného záření jsou absorbovány vodou. Z toho důvodu je potřebné data korigovat nahrazením jejich části například výstupy z jiných měření, např. teodolitem či sonarem. Existují však postupy, pomocí kterých je možné geometrii koryt extrapolovat přímo z původních rastrů, a to na základě sklonů břehů v rámci příčných profilů. V rámci této práce se vychází z postupu linear and double-linear estimation method podle Mersela a kol. [1].

Předložená práce představuje úvodní krok směrem k využití podobných extrapolačních postupů. Celkem 82 profilů bylo geodeticky zaměřeno a následně byly extrahovány příčné profily z rastru DMR 5G, na nichž byla prováděna extrapolace. Na dosavadním souboru příčných profilů se ukázalo, že extrapolační metoda vede k mírnému nadhodnocování minimální úrovně dna koryt oproti skutečně zaměřeným hodnotám. Z toho důvodu bylo také zjišťováno, nakolik je potřeba úhly sklonů břehů zvýšit, aby bylo dosaženo dobré shody se skutečně naměřenými daty. Podstatné však je, že srovnávání bylo prozatím prováděno čistě na základě shody nejnižší úrovně dna v příčném profilu, nikoli z hlediska vlivu na výsledky hydrodynamického modelování.

Úvod

Modelování v hydrologii je kromě dobré znalosti a simulace fyzikálních procesů ovlivňováno významně i nepřesnostmi vstupních dat. Nejistotami v hydrologickém modelování se zabývala řada prací [2–4]. Zdroje nepřesností mohou plynout například z hodnot průtoků odvozených prostřednictvím hydrologického modelu, v němž již vstupní data (např. srážkové úhrny či vlhkost půdy) vykazují určité nepřesnosti [5]. Pokud je průtok odvozován z měření vodních stavů, je přesnost ovlivněna kvalitou vztahu vodní stav/průtok [2, 6]. Problematickým faktorem při modelování povodňových rozlivů je také nastavení hodnoty součinitele drsnosti [7–9] a geometrický popis koryta a říční nivy (např. [10–16]).

Obr. 1. Ukázka měřeného příčného profilu na úseku Husího potoka ve Vlkovicích u Fulneku
Fig. 1. An example of a measured cross-section profile on the Husí brook in Vlkovice near Fulnek

Problematice přípravy kvalitního digitálního modelu terénu (DMT) je v hydrologii věnováno značné úsilí. Zpřesňování DMT je možné provádět pomocí různých přístupů, především interpolací geodeticky zaměřených příčných profilů koryta či interpolací samostatně zaměřených bodů batygrafie a jejich integrací s okolním terénem [2]. Značného pokroku v rámci modelování obecně bylo dosaženo zavedením technologie leteckého laserového snímkování terénu (z angl. Light Detection and Ranging – akronym LiDAR). Jedná se o technologii, která umožňuje měřit zejména nadmořskou výšku povrchu (tzv. topo LiDAR system) [17, 18]. Měřená data jsou ukládána ve formě mračna bodů [19]. I přes značné zlepšení může být přesnost měřených dat omezena. Laserový paprsek nemusí vždy proniknout až k zemskému povrchu v případě husté vegetace či zástavby. Navíc může docházet k pohlcování laserového paprsku vodou [20]. Absence topografie vodou vyplněných částí vodních útvarů přitom představuje významný problém z hlediska modelování hydrauliky proudění [11, 13, 14]. Z toho důvodu byl kromě technologií, jako je sonar [21], digitální fotogrammetrie [22] či satelitní měření [23], vyvinut typ LiDARu umožňující i měření batygrafie (bathymetric LiDAR system). Na rozdíl od tradičního LiDARu, využívajícího blízké infračervené záření, používá vlnové délky zelené části spektra, které pronikají vodou [24].

Pro eliminování chyb spojených s využíváním konvenčních měření LiDARem (výstupem takového měření je i sada DMR 4G a DMR 5G) vznikla řada extrapolačních metod pro určení topografie části koryt, resp. příčných profilů koryt, vyplněných vodou. Základní a nejjednodušší metodou je tzv. linear a double-linear method [1, 25], spočívající v extrapolaci sklonu břehů směrem do koryta toku. Hlavním cílem tohoto článku je: 1. provést prvotní srovnání výstupů obou zmíněných extrapolačních metod s geodeticky zaměřenými příčnými profily koryt z hlediska dosažení minimální úrovně dna, 2. nalézt pro každý příčný profil vhodný násobek sklonu břehů takový, aby analogickou aplikací uvedené metody bylo dosaženo co nejlepší shody s měřenými profily.

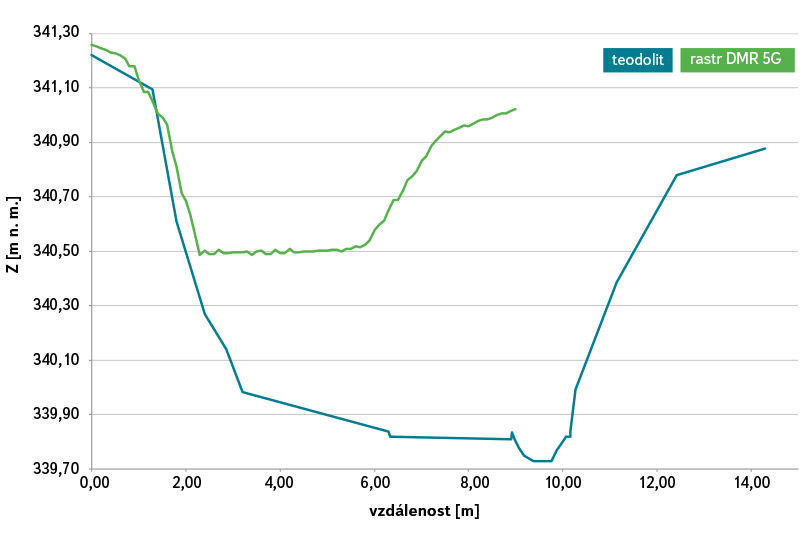
Obr. 2. Srovnání příčného profilu koryta Husího potoka ve Vlkovicích zaměřeného teodolitem a extrahovaného z DMT DMR 5G
Fig. 2. Comparison of cross-section profiles on the Husí brook in Vlkovice measured by theodolite and extracted from the DMT DMR 5G

Vstupní data a metodika

S využitím celkem 82 příčných profilů menších vodních toků byla analyzována přesnost dosažení minimální úrovně dna koryt (obr. 1). Jejich skutečný (referenční) tvar byl zaměřen pomocí teodolitu a GPS stanice v rámci projektu NAKI [26] a KUS. Souřadnice všech takto zaměřených bodů byly importovány do prostředí ESRI ArcGIS 10.3.1, kde byly na jejich základě vykresleny linie všech příčných profilů. Digitální model terénu (DMT) byl vytvořen z datové sady ČÚZK DMR 5G vzniklé leteckým laserovým snímkováním povrchu v letech 2009 až 2013 [27]. Z mračna diskrétních bodů rozmístěných v nepravidelné trojúhelníkové síti (angl. triangulated irregular network – TIN) o souřadnicích X, Y, H, kde H je nadmořská výška ve výškovém referenčním systému Balt po vyrovnání (Bpv).

Tabulka 1. Charakteristiky přesnosti DMR 5G na různém povrchu a půdním krytu (převzato z Technické zprávy k Digitálnímu modelu 5. generace, ČÚZK, 2016)
Table 1. Accuracy characteristics of the of the DMR 5G dataset for various types of surfaces (according to the Technical report of the digital model of relief 5^th generation)

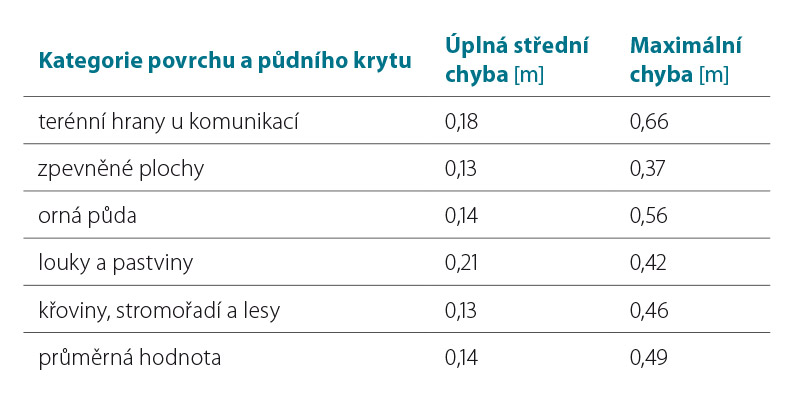
Chyby výšky pro různé typy povrchu v rámci datové sady DMR 5G jsou přehledně uvedeny v tabulce 1. Kromě deklarovaných nepřesností je negativní vlastností DMT vytvořeného z této datové sady rovněž nepřesná, resp. neúplná, topografie koryt vodních toků. To je zapříčiněno nepropustností vody pro laserový paprsek dané vlnové délky. Terén vodních ploch je proto interpolován z bodů bezprostředně přiléhajících k vodnímu útvaru.

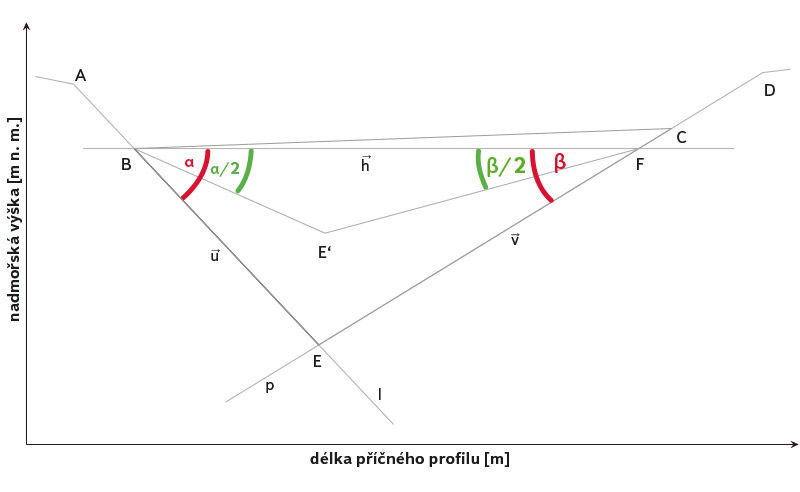
Obr. 3. Schématické znázornění extrapolace metodou linear a double-linear (podle Mersela a kol. [1])
Fig. 3. Schematic representation of linear and double-linear estimation method (according to Mersel et al. [1])

Prvním krokem k vytvoření spojitého DMT v prostředí ESRI ArcGIS z bodové vrstvy byla konstrukce TIN pomocí nástroje Create TIN bez omezení Delaunayho triangulace. Tento TIN byl následně pomocí nástroje TIN to Raster převeden na rastr s velmi jemným rozlišením 0,10 m. Údaje o nadmořské výšce byly přeneseny z podkladového rastru DMT do borové vrstvy příčného profilu pomocí nástroje Extract Values to Points (obr. 2).

Extrapolace koryta

Metody lineárního odhadu

Nejjednoduššími způsoby odstranění zmíněných nedostatků jsou metody lineárního a dvojitého lineárního odhadu (linear and double-linear estimate method) [1]. Tyto metody jsou založeny na lineární extrapolaci linie terénu na obou stranách příčného profilu. Nejnižší bod koryta je dán průsečíkem obou extrapolovaných linií (obr. 3). Je zřejmé, že takto extrapolovaná hloubka je závislá na šířce koryta a na úhlech sklonu α, β obou břehů. Velikost úhlů α, β je vypočítána na základě vymezení břehů (levý břeh – body A, B; pravý břeh – body C, D). V rámci studie bylo využito obou výše uvedených metod. Při metodě lineárního odhadu jsou velikosti úhlů α, β zachovány a nejnižším bodem příčného profilu je bod E. Metoda dvojitého lineárního odhadu spočívá ve snížení úhlů α, β na polovinu původní velikosti. Nejnižší bod je označen E‘. Průsečík vodorovné přímky se směrovým vektorem h ⃗, procházející bodem B, s přímkou p je bod F.

Výpočet průsečíků E, E‘ se skládá z několika kroků:

1. Převod souřadnic bodů z kartografických na relativní

Souřadnice systému S-JTSK Křovák East North byly nahrazeny vzdálenostmi daného bodu od počátku příčného profilu.

2. Sestavení obecných rovnic přímek obou břehů

Ze souřadnic bodů A, B, C, D byly odvozeny vektory u ⃗ a v ⃗, což jsou směrové vektory přímek l, p.

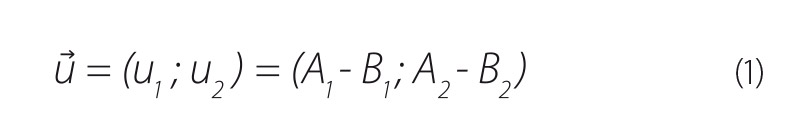
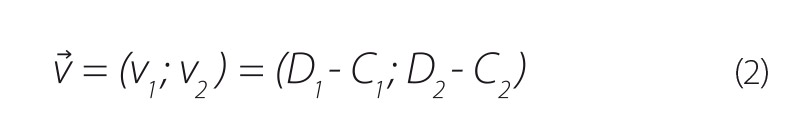
Obecné rovnice přímek l, p mají tvar:

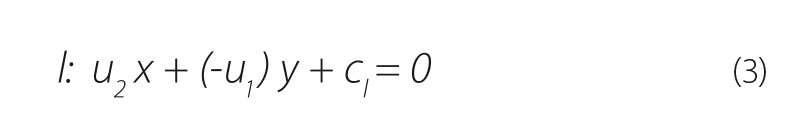
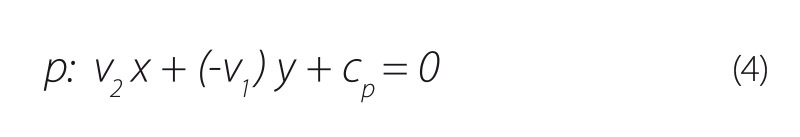
3. Výpočet průsečíku přímek obou břehů

Řešením soustavy rovnic (3) a (4) jsou souřadnice bodu E [X_E; Y_E]. Souřadnice Y_E určuje nadmořskou výšku průsečíku při použití metody lineárního odhadu.

4. Výpočet úhlů sklonů obou břehů

Zjištění úhlů α, β vychází ze vztahu pro kosinus úhlu dvou nenulových vektorů. Při znalosti směrových vektorů u ⃗ a v ⃗ přímek l, p postačí zvolit libovolný vektor h⃗ v horizontálním směru (např. h⃗  = (1; 0)). Pak pro úhel α platí, že:

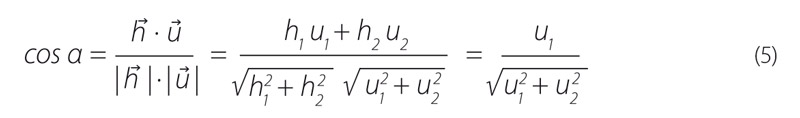
a pro úhel β:

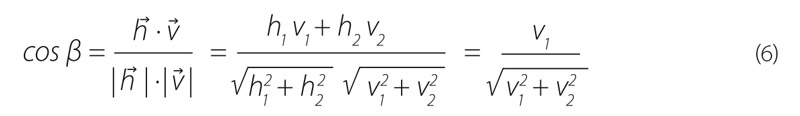
5. Výpočet průsečíku při polovičních úhlech

Bod E‘ [E‘₁; E‘₂] je průsečíkem přímek, které svírají s vektorem h ⃗ úhly α/2, β/2. Při výpočtu souřadnic bodu je možné vycházet ze směrnicových rovnic přímek l a p, které mají tvar:

Kde čísla k_l, k_p jsou směrnice přímek l, p. Obecně platí, že směrnice k dané přímky je rovna tangentě úhlu, který tato přímka svírá s kladnou poloosou x. Z toho plyne, že ze vztahů (7), (8) je možné sestavit rovnici:

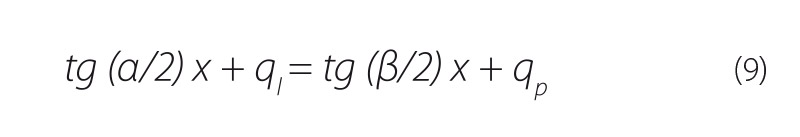
z níž je možné vypočítat výsledné souřadnice. Pro uvedený vztah však musí být současně splněny tyto podmínky, které jsou zřejmé z obr. 3:

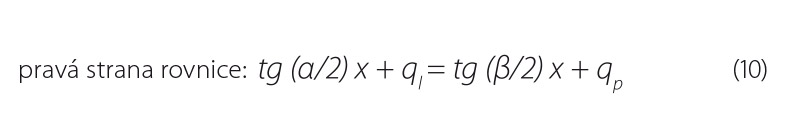
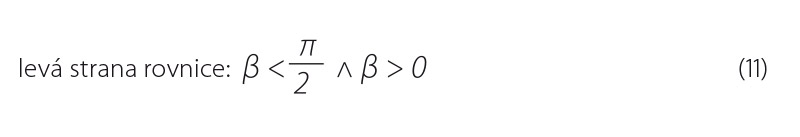
6. Výpočet odchylek od zaměřené nejnižší úrovně dna

Pro obě extrapolační metody jsou nakonec vypočítány odchylky úrovně průsečíků přímek obou břehů od Z_min.

Metoda n-násobku úhlů

Metoda n-násobku úhlů je založena na hledání čísla n takového, aby jeho součin s úhly α, β určoval optimální úhly směrových vektorů přímek vůči h ⃗. Průsečíkem těchto přímek l, p by měl být bod Z [Z₁; Z₂], jehož souřadnice Z₂ se bude svou hodnotou blížit Z_min příslušného příčného profilu (obr. 4).

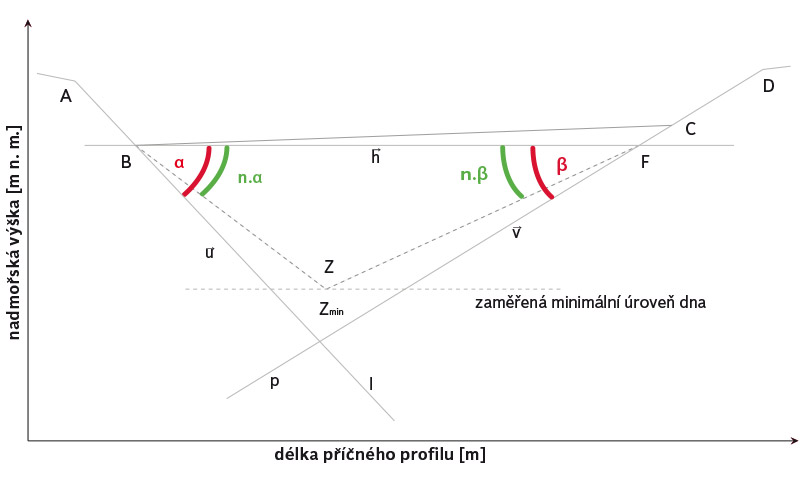
Obr. 4. Schématické znázornění metody n-násobků úhlů α, β
Fig. 4. Schematic representation of the method of multiplier n

Při odvození vztahu pro výpočet čísla n je nutné vycházet ze směrnicových rovnic přímek l, p (7), (8). Čísla k_l, k_p jsou směrnice přímek l, p. Obecně platí, že směrnice k přímky je rovna tangentě úhlu, který svírá přímka s kladnou poloosou x. Z toho plyne, že ze vztahů (7) a (8) je možné sestavit rovnici:

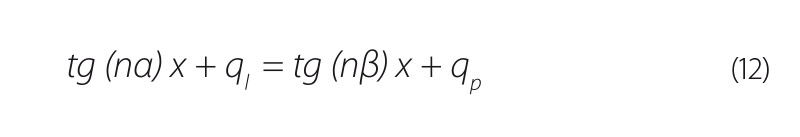
I zde musí současně platit podmínky:

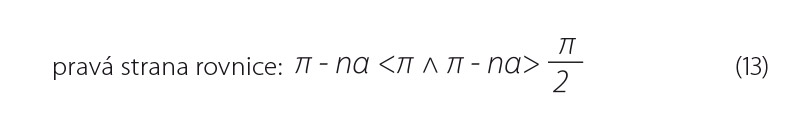
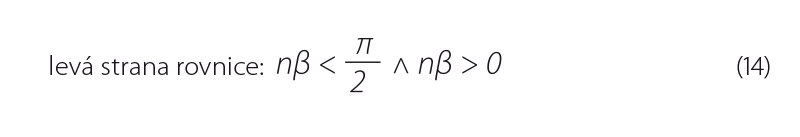
Je-li známo, že otáčející se přímka l prochází bodem B a přímka p bodem C, umožňuje vztah (12) pro každý příčný profil najít optimální hodnotu čísla n, a tím přiblížení k Z_min daného příčného profilu.

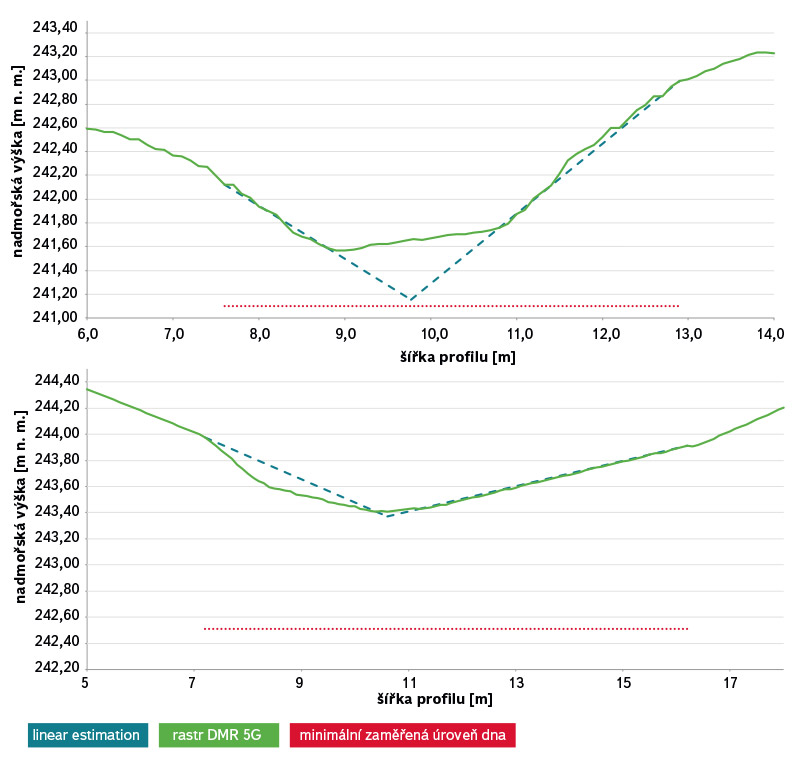
Obr. 5. Příklad příčného profilu s dobrou shodou (nahoře), neshodou minimální úrovně koryta extrapolovaného pomocí metody linear estimation (dole) [1]
Fig. 5. An example of a cross-section showin good match (above), discrepancy of the minimal level of channel bottom extrapolated by the linear estimation method (down) [1]

Uvedený problém je možné řešit více způsoby. V rámci této studie bylo využito programovacího jazyka Python. Základem sestaveného kódu je rovnice (9), do níž vstupují násobky původních úhlů α, β. Obecně je tedy výpočet založen na zvyšování n od minima, plynoucího z podmínek (13) a (14), o velmi malý krok (např. 10^-5). Přitom je nutné zajistit opakované přepočítávání hodnot nα, nβ, q_l, q_p a souřadnice Z₂, která určuje nadmořskou výšku průsečíku. V okamžiku, kdy je poprvé zaznamenána hodnota Z₂ nižší než Z_min, výpočet se zastaví a hodnota n se sníží o hodnotu jednoho kroku, pro který je rovněž zjištěna hodnota Z₂. Nakonec je vybrána ta hodnota n, při níž je absolutní hodnota rozdílu vůči Z_min menší.

Výsledky

Analýza zpracovaných příčných profilů ukázala, že při využití lineární extrapolační metody podle Mersela a kol. [1] je možné dosáhnout poměrně reálného údaje minimální úrovně dna Z_min. Mezi jednotlivými profily však byla zaznamenána značná variabilita (obr. 5). Dokládají to údaje uvedené v tabulce 2. Průměrná odchylka minima činí +0,16 m, hodnota mediánu +0,71 m a směrodatná odchylka +0,77 m. Z toho vyplývá, že tato extrapolační metoda z hlediska průměru úroveň dna spíše nadhodnocuje. Je tedy zřejmé, že snížením sklonu břehů na polovinu původní hodnoty žádného zlepšení dosáhnout nelze. Pro úplnost jsou však i pro tuto extrapolaci hodnoty základních popisných statistik uvedeny. Pro přehlednost jsou na obr. 6 vyobrazeny krabicové grafy odchylek extrapolované minimální úrovně dna od minima zaměřeného v terénu při aplikaci obou uvedených metod.

Tabulka 2. Popisné statistiky odchylek nejnižší úrovně extrapolovaného dna vůči Z_min při použití metody linear, double-linear a násobku n sklonů břehů příčných profilů
Table 2. Descriptive statistics‘ overview – deviations of the lowest level in the extrapolated cross sections using the linear, double-linear estimation method [1] and multiplier n method from the in situ geodetic measurements

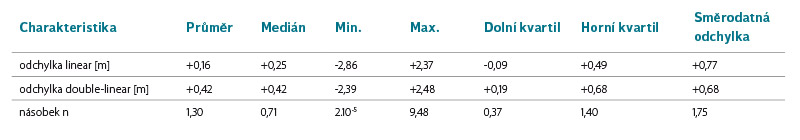
Dále se ukázalo, že výsledná odchylka dosažené minimální úrovně příčných profilů vůči úrovni Z_min vykazuje určitou závislost na součtu úhlů břehů α + β. Obecně se dá tvrdit, že pro nízké hodnoty součtů sklonů břehů dochází převážně k nadhodnocení minimální úrovně dna extrapolovaného koryta a naopak (obr. 7). Hodnota korelačního koeficientu činí 0,64 (tj. střední závislost). Největší shody je dosahováno nejčastěji v rozmezí hodnot součtu α + β přibližně 0,8 až 1,0 rad (tj. přibližně 45° až 57°). Nicméně, pro jednoznačnější výsledky by bylo potřebné shromáždit větší soubor příčných profilů.

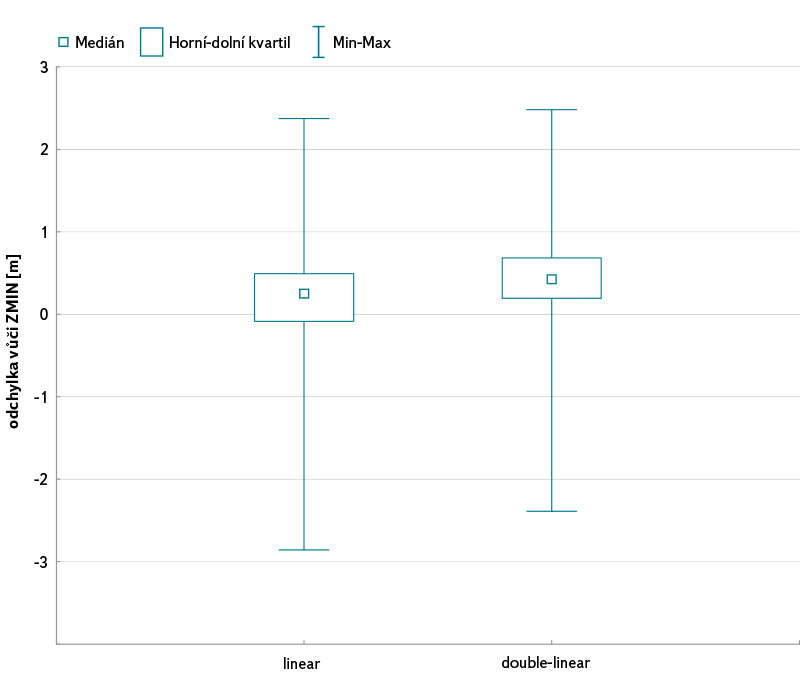
Obr. 6. Krabicový graf odchylek nejnižšího bodu extrapolovaného dna vůči Z_min zaměřené geodeticky
Fig. 6. Boxplot of the deviations of the lowest level in the extrapolated cross sections using the linear and double-linear estimation method [1] from the in situ geodetic measurements

Snahou bylo také nalézt optimální hodnotu násobku n úhlů α, β. Postupem blíže popsaným výše bylo zjištěno, že průměrná hodnota násobku n činí pro soubor osmdesáti dvou profilů 1,30, hodnota mediánu je 0,71. Krabicový graf charakterizující rozložení hodnot n je uveden na obr. 8. Závislost rozložení těchto hodnot na poměru sklonů obou břehů α, β, jejich součtu ani poměru se neprokázala.

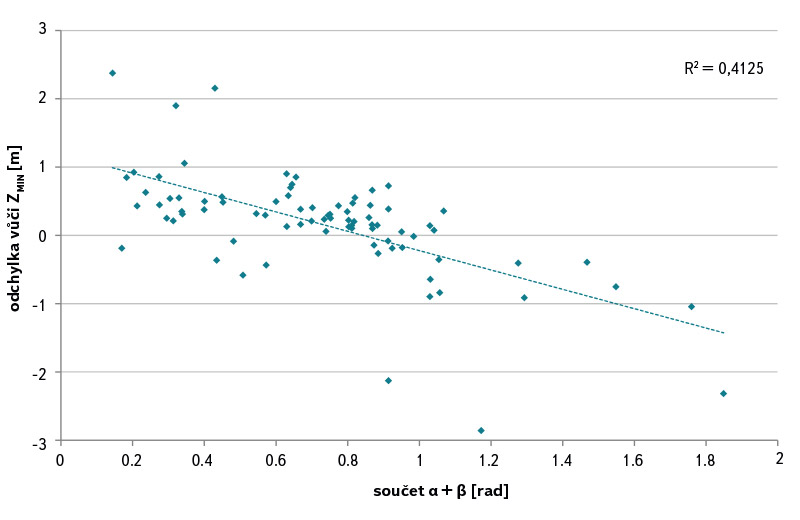
Obr. 7. Vztah odchylky nejnižší úrovně dna koryt extrapolovaných metodou linear a součtu sklonů břehů α + β příčných profilů
Fig. 7. Relationship of the deviations of the lowest level in the extrapolated cross sections using the linear and double-linear estimation method [1] from the in situ geodetic measurements and sums of banks‘ slopes for each cross sectio

Závěr

Aplikace metody lineárních extrapolací břehů koryt z DMT vytvořeného z datové sady DMR 5G za účelem nalezení minimální úrovně koryta ukázala, že tato metoda v převážné části případů vede k mírnému nadhodnocování minimální úrovně dna (průměrně o +0,16 m). Z toho plyne, že vhodným krokem vedoucím ke zpřesnění by bylo zvýšení sklonů břehů o jistý násobek n (pro konkrétní analyzovaný soubor profilů je to průměrně 1,30). Do úvahy je však nutné brát skutečnost, že úspěšnost interpolace zde není hodnocena vzhledem k výstupům hydrodynamického modelování, ale čistě vzhledem k nejnižší úrovni koryt vodních toků. V tomto duchu je potřeba k této studii a jejím výsledkům přistupovat.

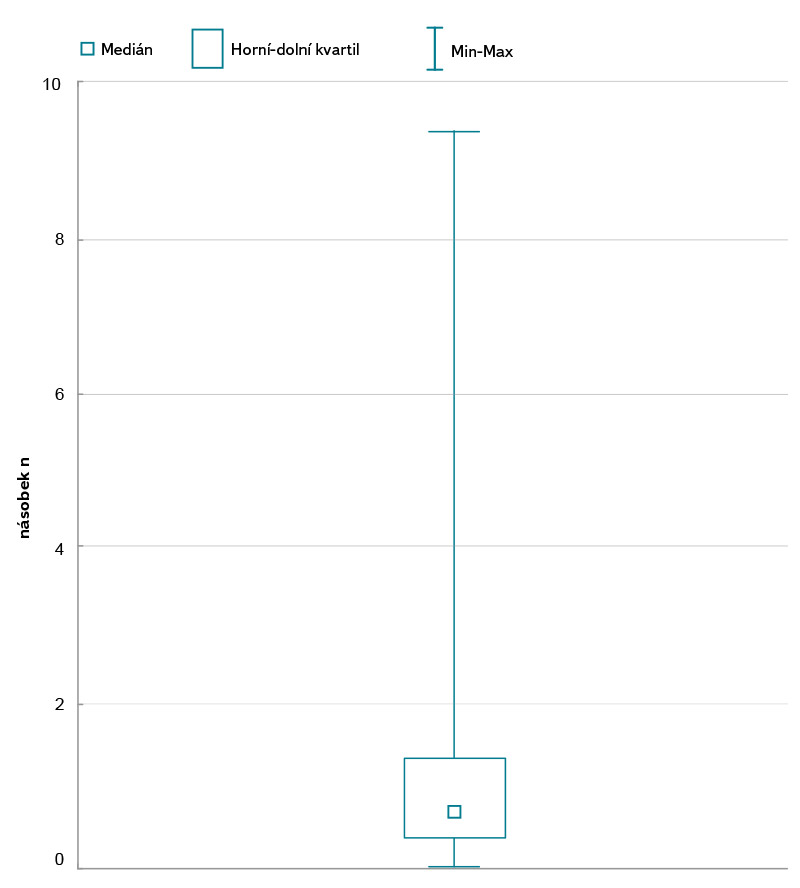
Obr. 8. Krabicový graf optimálních násobků n sklonů břehů α, β
Fig. 8. Boxplot of optimal values of multiplier n

Problematickým aspektem extrapolační metody je kromě již zmíněných chyb datové sady DMR 5G (úplná střední chyba, maximální chyba) také subjektivita vymezení břehů koryt, resp. jejich počátečních a koncových bodů. Vymezení může být v jednotlivých případech nejednoznačné s ohledem na proměnlivost sklonů. Další limitující skutečností je zatím poměrně omezený vzorek příčných koryt a úseků toků, pro které byla analýza provedena. K podrobnějšímu hodnocení metody by bylo žádoucí soubor příčných profilů významně rozšířit a zohlednit při tom i variabilitu koryt z hlediska jejich geometrie a z ní vyplývající nepřesnosti digitálního modelu terénu v úrovni koryta (bystřiny, zarostlá koryta, koryta s podemletými břehy, koryta se svislými břehovými zdmi, lichoběžníková koryta aj.). To by umožnilo detailně analyzovat vzájemné vztahy mezi výsledky extrapolačních metod a lépe identifikovat parametry příčných profilů a jejich kombinace ovlivňující úspěšnost extrapolace koryta. Díky tomu bude možné vyvinout robustní metody extrapolace koryt definovaných parametrů z podkladů, kde úplná topografie koryt vodních toků není vykreslena.