Summary
The following article summarises the results of testing a method for the characterisation of water use in the system of life cycle assessment in the Czech Republic. The chosen method allows for robust expression of water use in the equivalent values of the reference system. The method is based on the potential renewability of water resources. To apply the method in the Czech Republic, characterisation factor values were derived for individual hydrological third‑order catchments in the Czech Republic. These values were compared with values calculated for specific profiles from the Czech Hydrometeorological Institute. In addition, water footprint of electricity production process in selected power plants and heat plants in the Czech Republic was determined by using a tested method. Given the fact that the chosen method does not cover the issue of impacts on human health and ecosystems, the identified values represent (only) the ‘‘water scarcity footprint of electricity and heat production processes in power plants and heat plants.’’

Introduction
‘‘Water footprint’’ is a technical term which started to appear in water management practice from the 1990 s. Water footprint was defined as the total amount of water used directly or indirectly for production, including consumed and polluted water [1]. This concept received some criticism, which pointed to the fact that such a defined water footprint tells us nothing about the impacts that water use brings. The community involved in life cycle impact assessment came up with its own understanding of the concept of water footprint and the International Organization for Standardization (ISO) developed and issued a norm classifying water footprint in the category of life cycle impact assessment [2]. In Life Cycle Inventory (LCI), all information regarding inputs and outputs is collected throughout the life cycle of the examined product system. In relation to the water footprint, it then finds the amount of water used or consumed during the life cycle. Subsequently, during the Life Cycle Impact Analyses (LCIA) phase, the determined quantity of used or consumed water is transferred via the so‑called characterisation factors to the units expressing the so‑called ‘‘midpoint’’ impact categories [3]. One of the factors commonly used for ‘‘water consumption’’ characterisation is the Water Stress Index (WSI) [4]. However, there are many other characterisation factors [5]. Although the concept of Water Stress Index is commonly incorporated into leading LCA databases, it is criticised [6] in that it is a synthetic measure based on the results of hydrological models with problematic physical expression, which do not differentiate between water sources (precipitation, groundwater, surface water).
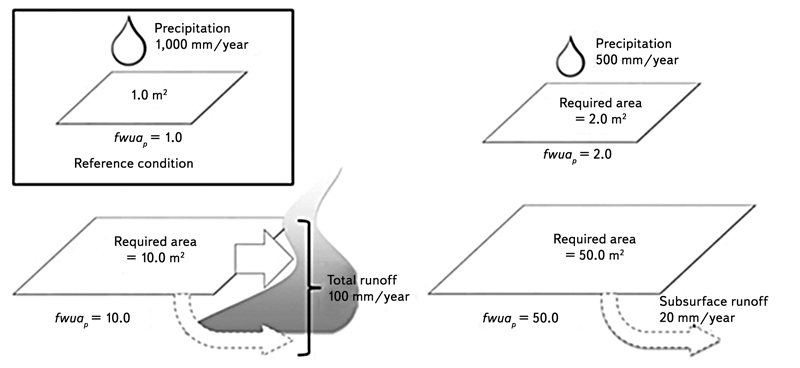
Fig. 1. Conceptual diagram of the water unavailability factor in terms of the required land area (reproduced with permission from: [7])
This figure is distributed under the Creative Commons Attribution License (CC BY 4.0).
In response to some of the deficits of the Water Stress Index, a method was published in 2015 [7] which is based on the assessment of water sources renewability in the selected area. Unlike Water Stress Index (and other similar characterisation methods), this method does not use the value of water use in the selected area for constructing the characterisation factor, so situations cannot occur where water use is calculated ‘‘twice’’ [6]. Other advantages of the method include the ability for spatial and temporal differentiation, as well as differentiation of various types of sources.
Methodology
Description of the tested method
The idea of a characterisation factor built on the renewability of water sources is based on the assumption that the impact of the use of the unit amount of water is inversely proportional to the ability of the source to supply or substitute this amount. Precipitation is virtually the only water source. In a catchment with water or precipitation scarcity, a larger area or a longer time must be available to create the desired amount of water. In other words, the potential impact can be expressed as a catchment area or the time required to obtain a unit amount of water from each water source. The characterisation factor is defined by equation 1.
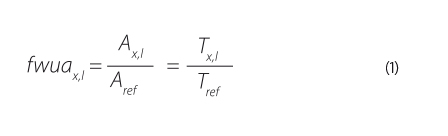
| where | fwuax,l | is | the characterisation factor of ‘‘water unavailability’’ for a source x in a location l, |
| Ax,l | the area required to obtain the unit amount of water at a defined time from a source x in a location l, | ||
| Aref | the area required to obtain the unit amount of water at a defined time under reference conditions, | ||
| Tx,l | the time required to obtain the unit amount of water from a defined area from a source x in a location l, | ||
| Tref | the time required to obtain the unit amount of water from a defined area under reference conditions. |
Factors Ax,l and Tx,l are defined by equations 2 and 3.


| where | QA,ref | is | the reference water quantity per unit of time [m3/year], |
| QT,ref | the reference water quantity per unit of area [m3/m2], | ||
| Px,l | the annual capacity of a water cycle to restore a source x in a location l [m/year]. |
Reference water quantity may have any value. To determine the reference value [7] the authors of the method proceed from the approximate global precipitation average per 1 m2 of the Earth’s surface, which is approximately 1 000 mm. They use this value to express the characterisation factor for precipitation as well as surface water and groundwater sources, explaining that all sources of fresh water come from precipitation. Therefore, they consider the global average precipitation value to be an appropriate indicator for weighing renewability of water sources (in this sense, fossil groundwater without the possibility of replenishment from precipitation, which does not occur in the Czech Republic anyway, is not considered a renewable source). The resulting water footprint, determined by this method, is expressed in m3 H2Oeq., which can be physically interpreted as a reference precipitation amount, and, in the case of using reference values proposed by the authors of the method, as the amount of average precipitation on the Earth.
The total runoff can be considered as corresponding to natural recharge capabilities of groundwater from precipitation. The total runoff is composed of two components: direct and primary runoff. Direct runoff is formed from precipitation and primary runoff means the part of the total runoff which comes from groundwater sources. The amount of direct as well as primary runoff is defined by the hydrological cycle and can be considered as the theoretical maximum amount usable by society (note: this assumption neglects the requirement to maintain ecological flows, whether they are defined in any way; at the same time, however, it is not fundamentally contrary to the idea of grey water footprint [1]).
Table 1. Example of water scarcity footprint calculation (source: [7])
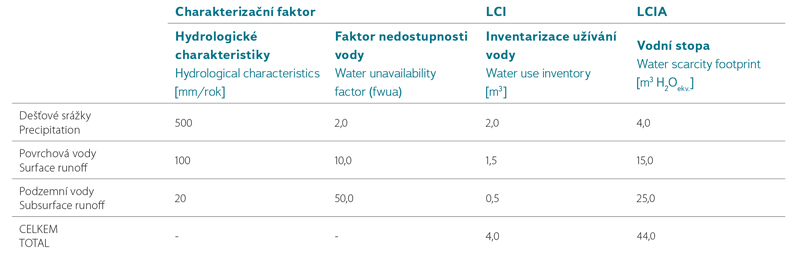
With a precipitation of 1000 mm/year, 1 m2 and 1 year is required to achieve the reference value of 1 m3. The water unavailability factor fwua = 1.0. For an explanation of method application, let us consider a catchment area of 1 km2, precipitation of 500 mm/year, surface water runoff of 100 000 m3/year and basic runoff 50 000 m3/year. In this catchment with precipitation of 500 mm/year, either an area of 2 m2 or a time of 2 years is required to achieve a reference volume of 1 m3. The characterisation factor of precipitation (p) fwuap= 1000⁄500 = 2. If the runoff level from the catchment is 100 mm/year (e.g. in a catchment area of 1 km2 = 1 x 106 m2, 100 000 m3 runoff in a year), then the characterisation factor of surface water runoff (sw) fwuasw= 1000⁄100 = 10. Similarly, the characterisation factor of groundwater (gw) fwuagw= 1000⁄50 = 20.
The potential impact of water use in the catchment can then be calculated for each source by multiplying the sum of the usage of each resource by its characterisation factor according to equation 4.
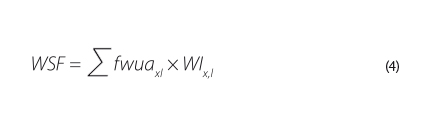
| where | fwuaxl | is | the characterisation factor of ‘‘water unavailability’’ for a source x in a location l, |
| WSF | the water scarcity footprint based on a potential impact [m3 H2Oeq.], | ||
| WIx,l | the result of the inventory analysis of water use based on water consumption in a source x in a location l [m3]. |
If for any product, service, institution or process at a described catchment, 2.0 m3 of rainfall, 1.5 m3 of surface water and 0.5 m3 of groundwater is consumed, the water scarcity footprint is 44.0 m3 H2Oeq. (see Fig. 1 and Table 1).
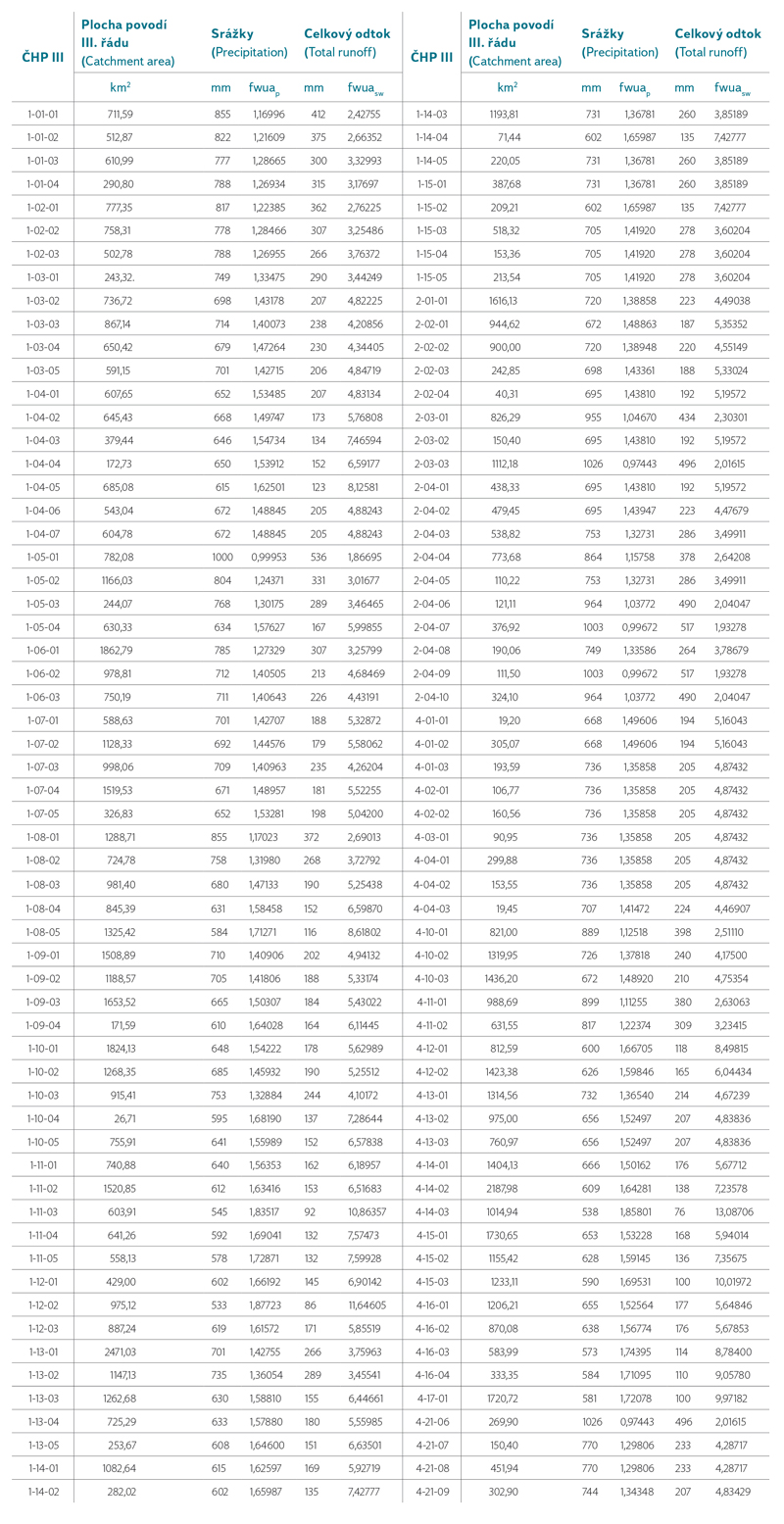
Characterisation factor values for third‑order catchments
The characterisation factor value fwuasw from equation 5 can be easily obtained from data provided by the Czech Hydrometeorological Institute (CHMI). However, in the case of LCA studies, it often happens that a large number of different water sources are used within the assessed life cycle, and obtaining data from CHMI would be rather expensive and time consuming. Therefore, a model approach was also tested to calculate characterisation factor fwuasw using hydrological characteristics of third‑order catchments derived by the BILAN model. Detailed procedures of hydrological characteristic determination is stated in a 2015 article [8]. Basic characteristics calculated using the BILAN model and used for processing the characterisation factor are the data on precipitation and total runoff related to the respective third‑order sub‑basin. For these characteristics, characterisation factor values fwuap and fwuasw were calculated (Table 2). As reference values for determining characterisation factors, a precipitation value of 1000 mm/year per area of 1 m2 was used, i.e. the same values as the authors of the tested methodology used [7]. The choice of these reference values will allow direct comparisons with other studies using the same ‘‘global’’ reference values.
Table 2. Factor of water unavilibility (fwua) for watershed 3rd order and reference fwuaref = 1.0
When dealing with larger catchments, consisting of several third‑order hydrological catchments, the value of the average characterization factor of the entire catchment fw͞u͞a͞sw is calculated according to equation 6. To compare the results obtained, 34 profiles with published hydrological data were selected [9]. The characterisation factor value fwuasw-CHMU from equation 5 was then determined from the available data of CHMI and compared with the calculated characterisation factor fw͞u͞a͞sw in the case of a composite catchment, or fwuasw.
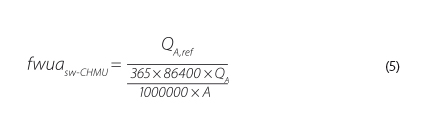
| where | fwuasw-CHMU | is | the average characterisation factor of ‘‘water unavailability’’ determined from CHMI data, |
| QA | the average flow through a CHMI station [m3/s], | ||
| A | the catchment area [km2.]. |
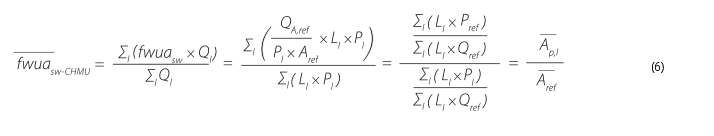
| where | fw͞u͞a͞sw | is | the average characterisation factor of ‘‘water unavailability’’ of surface water, |
| fwuasw | the characterisation factor of ‘‘water unavailability’’ of surface water in catchment l, | ||
| Ql | the annual runoff from catchment l [m3,], | ||
| Pl | the annual runoff level from catchment l [m], | ||
| Ll | the catchment area l [m2], | ||
| Pref | annual precipitation in reference conditions [m/year]. |
Power plant selection
Testing the method in the Czech Republic was based on information on the operational water consumption of selected Czech power plants. By permit analysis under Act no. 76/2002 Coll. (Integrated Pollution Prevention and Control), the third‑order catchments, which form a catchment of a power plant, were identified for each power plant (see Table 3). For each catchment of the power plant which is formed by two and more third‑order catchments, an ‘‘average’’ characterisation factor value fw͞u͞a͞sw was determined according to equation 6.
Table 3. Water scarcity footprint of Energy units (only power generation proces without downstream and upstream processes)
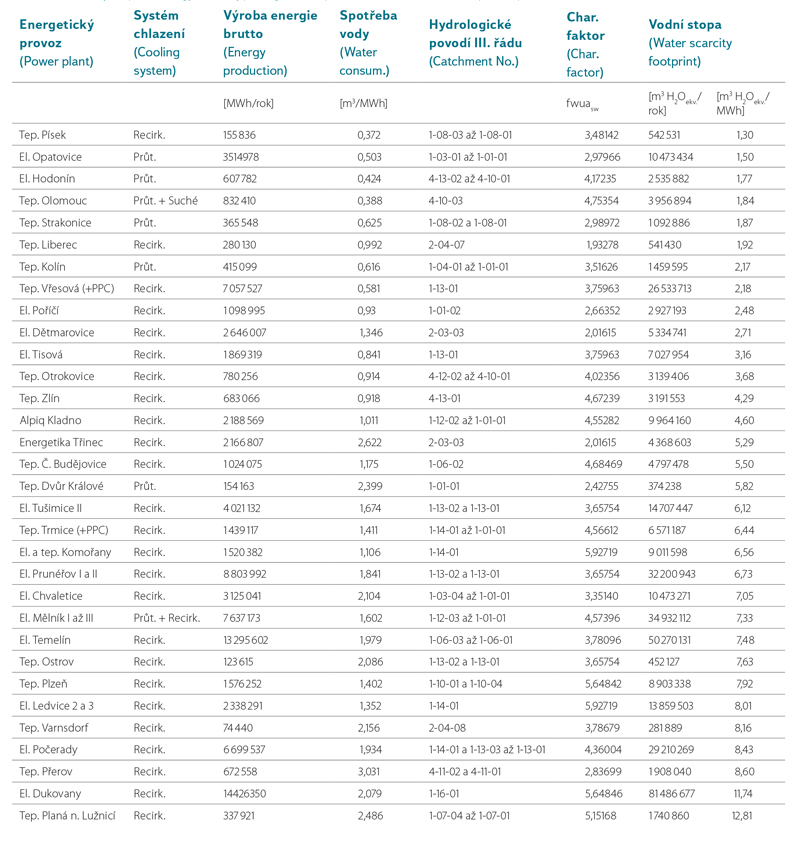
To evaluate the water footprint of power plants, the data on electricity and heat production in selected power plants were used, for which data were available on water consumption for electricity and heat production between 2004 and 2013 (see Table 3). Detailed information on the method of data processing can be found in a 2016 article [10].
Results
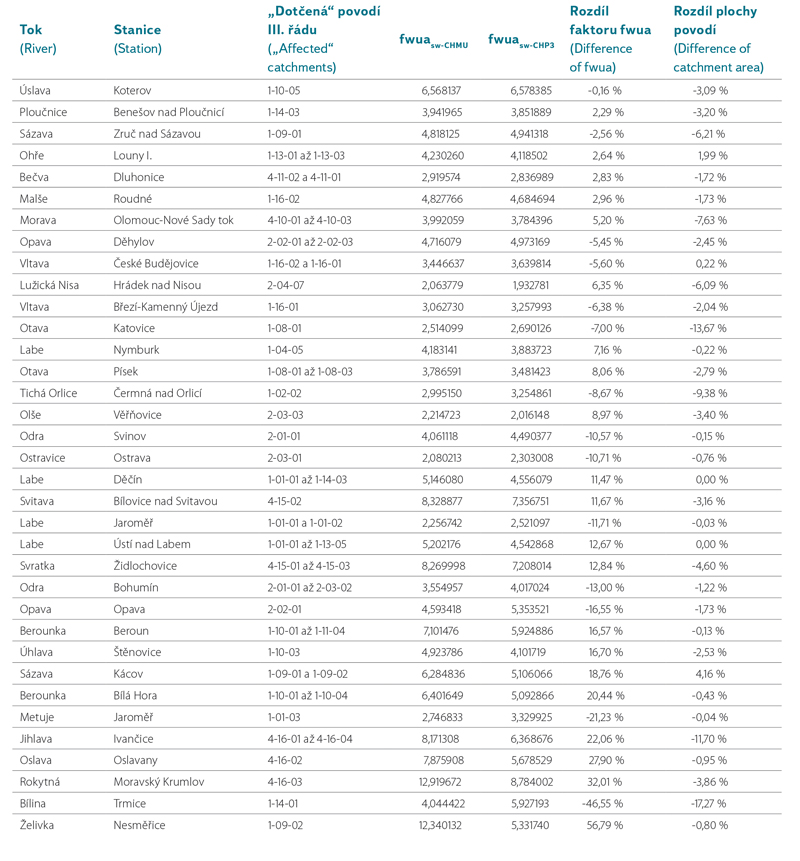
In the first part of our analysis, the values of calculated characterisation factors for third‑order catchments were compared with the values calculated directly from the data for specific profiles of CHMI. As indicated in Table 4, in 16 out of 35 profiles (46%) the differences between determined characterisation factors were up to ±10%. In other 8 profiles (23%), the difference of factor values ranges between ±10% and ±15%. Unfortunately, in four cases (11%) the difference is bigger than 25%.
However, the aim of this article is not testing the results of the hydrological model, but the description of possible applications of characterisation factor for assessment in the context of LCA studies. It can only be pointed out to future processors of LCA studies that using model outputs within the comprehensive evaluation of the LCA type is generally possible (and sometimes even necessary), but it is always vital to both verify and validate the data used and the results achieved. A probable explanation for high differences in some catchments lies in uncertainties with water use, because the modelled values correspond to the ‘‘natural’’ state, while the CHMI values are based on measured values and are therefore influenced by current water use.
The second part of our analysis dealt with the determination of the water footprint of selected power plants (see Table 3). The expected results were confirmed: the water footprint of power plants with once‑through cooling is generally lower than the water footprint of operations with recirculation cooling. The situation in both nuclear power plants suggests the importance of LCA evaluation. Although the specific consumption of both nuclear power plants is similar (1.979 or 2.079), the impact of electricity production in both plants is significantly different (7.48 or 11.74 m3 H2Oeq./MWh). Simply put, we can say that in the process of 1 MWh of power production in the Dukovany power plant, 11.74 m3 of reference quantity of water is needed, which was determined as ‘‘global average precipitation’’, while at the Temelín power plant it is only 7.48 m3.
Table 4. Comparison of values of characterisation factor of Czech Hydromet. Institute profiles computed from characteristics of profiles and characteristics of catchment
This is due to the fact that the Dukovany nuclear power plant lies on less water flow with a smaller catchment and lower runoff level. Therefore, although its specific water consumption for production of 1 MWh of power is only 105% of Temelín’s specific consumption, the water footprint of the process of 1 MWh of electricity and heat production is about 57.0% higher than the water footprint of the process of electricity and heat production in the Temelín nuclear power plant. It is important to realize, however, that these ratios apply only to the electricity and heat production sub‑process itself in a power plant. In regard to the fact that when testing the method, the water footprint of other processes within the life cycle was not determined (extraction of primary raw materials, their processing, transport, spent fuel management, distribution of produced power, etc.), these ratios cannot be related to the whole life cycle of both power plants.
The water footprint of the tested plants is then based on the amount of power produced and is expressed in m3 H2Oeq./year. The value thus obtained is, in layman’s terms, the amount of ‘‘global average precipitation’’ which are ‘‘consumed’’ in power plants per year. Again, it should be noted that this is only a one sub‑part of water footprint, which is related only to the process of energy production itself in a power / heat plant, i.e. it is not the value of the water footprint of the entire life cycle of electricity and heat production in these power plants.
Discussion
The tested method proved easy to use. For local LCA studies, it is possible to use average precipitation in the Czech Republic as a reference quantity instead of ‘‘global’’ precipitation. Using the average precipitation in the Czech Republic is recommended, especially for applications with a shorter time step, in monthly steps for example, when it is possible to consider real monthly precipitation as a reference, while in the case of ‘‘global’’ precipitation, 1/12 of the annual global precipitation can be used.
The authors of the method also assume that all water is available for use, which of course is only a theoretical assumption. In real conditions, it is not possible to use either all precipitation or the entire runoff from a catchment. From the perspective of application use, it is not a major problem, for example for surface runoff to subtract ‘‘minimal residual flow’’ or otherwise defined ‘‘ecological flow’’. In the case of groundwater and precipitation, however, this construction is not so clear. Moreover, by such extension a certain elegance of the proposed concept and the independence of the concept on subjective decision‑making is lost, since the decision about ‘‘what will be subtracted’’ is a subjective decision by the study investigator.
The principle of the method shows that the method is not entirely suitable for some applications, for example deciding on the impact on the availability of local water sources in different locations, since the results of the characterisation model are only linked indirectly to the actual water availability at the assessed location.
The data presented also do not include water loss by evaporation from reservoirs which are a part of water management of the individual power plants. In the case of Temelín nuclear power plant, the loss by evaporation from Hněvkovice reservoir is approximately 7% of the difference between withdrawal and discharge for the power plant. In the case of Dukovany nuclear power plant, evaporation from Dalešice – Mohelno reservoir is even around 14%. The different localisation of withdrawals and discharges was neglected for this testing purpose. It can play important role in real application of tested method. For example, nuclear power plant Temelín draws water from catchment 1-06-03 but discharges waste water to the catchment 1-07-05. These two catchments have the different hydrological condition and (of course) different value of characterization factor. In real study have to be withdrawals from catchment 1-06-03 calculated as losses and discharges to catchment 1-07-05 as gains with different values of characterization factor.
Conclusion
A characterization model based on the renewability of water sources has proved to be a readily usable tool, enabling the use both of data obtained by measuring (or derived from it) and the results of mathematical models. To facilitate the application of the method in practice, a table of characterisation factors of precipitation and total runoff for individual third‑order catchments was prepared. The testing showed that in the case of the input data from mathematical models, validation and verification of this data is important since for some catchments the results have an error exceeding ±10–15 %. Specific applications in selected 32 power and heat plants showed that the water footprint in terms of life cycle assessment is lower in plants with once‑through cooling as compared to plants with recirculation cooling.
The tested method does not address current use of water sources and assumes that the entire runoff is available to users. The tested method also does not address the issue of water degradation, the effect on ecosystems and on humans. For such life cycle impact assessment, it is necessary to use other characterisation methods. The results obtained using the tested method can be described only as water scarcity footprint.
Acknowledgements
The article was written within the project QJ1520322 ‘‘Procedures for compilation and verification of a water footprint in accordance with international standards’’ addressed with financial support from the Ministry of Agriculture (Program zemědělského aplikovaného výzkumu a experimentálního vývoje Komplexní udržitelné systémy v zemědělství 2012-2018 “KUS“ / Programme of agricultural applied research and experimental development Complex sustainable systems in agriculture 2012–2018). Characteristics of the third‑order catchments calculated by the BILAN model generated under the project Strategy for protection against negative impacts of floods and erosion phenomena of nature‑friendly measures in the Czech Republic, which is co‑financed by the European Union – the European Regional Development Fund, the State Environmental Fund and the Czech Ministry of Environment under the Operational Programme Environment. The data on the operational water consumption in thermal power plants and heat plants were prepared within the project TD020113 ‘‘Impacts of socio‑economic changes in society on water consumption’’ addressed with financial support from the Technology Agency of the Czech Republic within the programme.
