ABSTRAKT
Příspěvek se zabývá hydraulickou analýzou klapkového uzávěru v Doksanech a ve Strakonicích na základě vyhodnocení experimentálních měření realizovaných na fyzikálních a matematických modelech ve Vodohospodářském experimentálním centru Fakulty stavební ČVUT v Praze.
Měření v rámci jezu Doksany probíhala na fyzikálním modelu v měřítku 1 : 12,5 a na matematickém 3D modelu v programu Ansys CFX. Na obou modelech byly nastaveny standardní i mimořádné situace, tedy bez zavzdušnění a s překročením maximální provozní hladiny. Pro jez ve Strakonicích byl postaven fyzikální model v měřítku 1 : 7, na němž byly měřeny hladiny a průtoky pro běžné provozní stavy.
V souvislosti s klimatickou změnou dochází ke zvýšení četnosti intenzivních srážek, které častou vedou k náhlým povodním. Tyto extrémní meteorologické jevy představují riziko pro majetek a lidské životy. Vzhledem k této skutečnosti je nutné zpřesňovat přepadové součinitele, jež se používají ke stanovování konzumpčních křivek přelivů. Tyto konzumpční křivky používané v manipulačních řádech a automatizovaných řídicích systémech pak více odpovídají skutečnosti, což pomáhá při operativním řízení povodně přes vodní díla, např. k zdokonalení transformace na vodních nádržích, kdy je potřeba rychle a účinně rozhodovat o manipulacích na vodohospodářských soustavách a minimalizovat případné negativní dopady.
Cílem výzkumu je doplnit stávající křivky přepadových součinitelů pro vyšší stupeň zatopení a pro mimořádné situace. Součástí hydrotechnického výzkumu je porovnání různých typů rozražečů a matematický popis pohybu klapky.
ÚVOD
Klapkové uzávěry jsou dnes nejčastějšími pohyblivými uzávěry, s nimiž se můžeme setkat u jezů či přehrad v České republice (ČR). Zároveň lze o klapkových uzávěrech říci, že díky svým výhodám, zejména možnosti jemné manipulace či ekonomické výhodnosti jejich vybudování i provozu, byl a je tento typ uzávěru nejpoužívanější v rámci rekonstrukcí jezů Labsko-vltavské vodní cesty či dalších jezů v ČR a bezpečnostních hrazených přelivů přehrad, např. vodního díla Nechranice.
Klapkové uzávěry byly předmětem výzkumu Jaroslava Čábelky, Gerharda Wickerta i Gerharda Schmaussera na konci 20. století [1, 2]. V těchto publikacích se však autoři věnují pouze standardním stavům bez velkého vlivu zatopení dolní vodou.
Z tohoto důvodu a s ohledem na zrychlující se vývoj klimatické změny, který přináší častější výskyt extrémních srážek, bylo přistoupeno k doplnění českého výzkumu o běžné stavy s vyšším ovlivněním dolní vodou a současně o mimořádné situace. Mimořádnými situacemi je myšlen stav úrovně hladiny vodního toku, kdy hladina při zvýšeném průtoku stoupne nad úroveň provozní hladiny, anebo stav, kdy dojde u klapkového jezu k zanesení zavzdušňovacího potrubí, což vede k vyšší průtočnosti přes hradicí konstrukci.
METODIKA
V rámci výzkumu byly postaveny výsekové fyzikální modely jezů s nasazenými klapkovými uzávěry ve Vodohospodářském experimentálním centru Fakulty stavební ČVUT v Praze. Současně byly vytvořeny matematické 3D modely pro jeden z jezů. Cílem bylo analyzovat hydraulické chování přelivů při různých průtocích, geometrických změnách na přelivné hraně klapkového uzávěru a proudění vody v okolí přelivů. Z naměřených a vypočtených hodnot byly získány průběhy hladin, jež bylo možno porovnat napříč mezi jednotlivými metodami, včetně numerických výpočtů dle grafů stávajících výzkumů.
DATA
Vodní dílo Doksany
Vodní dílo Doksany (obr. 1) leží na vodním toku Ohře v jižní části obce Doksany v Ústeckém kraji. Součástmi vodního díla jsou strojovna, jez, malá vodní elektrárna a rybí přechod. Jez je tvořen železobetonovou konstrukcí, na které je umístěna pohyblivá hradicí konstrukce, tj. ocelový uzávěr – jezová dutá klapka. Klapkové uzávěry mají na přelivné hraně umístěny velké rozražeče profilu U a malé rozražeče profilu L. Vzdouvací objekt má dohromady dvě pole přelivu, přičemž obě mají délku 20 m a kóta pevného přelivu je 150,81 m n. m. Maximální hladina jezové zdrže je podle manipulačního řádu na kótě 153,25 m n. m. U každého jezového pole je v pilíři vedeno zavzdušňovací potrubí DN300 a otvor pro aretační čep klapky. V podjezí se nachází 13,2 m dlouhý vývar, hluboký 1,6 m a zakončený třemi stupni a zvýšeným prahem, jenž je o 0,3 m výše nad opevněným dnem. Prostor koryta kolem jezu je opevněn kamennou dlažbou a ukončen kamenným záhozem. Nutno podotknout, že výškový rozdíl mezi dnem nadjezí a podjezí je 1 m, což výrazně zamezuje vyššímu ovlivnění přepadu zatopením dolní vodou.

Obr. 1. Jez Doksany
Fig. 1. Doksany weir
Vodní dílo Strakonice
Vodní dílo Strakonice – nebo také stabilizační jez Strakonice – leží na vodním toku Otava ve městě Strakonice v Jihočeském kraji. Stavba je tvořena železobetonovou jezovou konstrukcí o dvou polích s délkou 20 m, na níž je uložena dvojice klapkových uzávěrů s násoskami nasazenými vždy mezi příčnými výztuhami a se zdvihacím mechanismem, strojovnami nad pilíři a sportovní propustí, jež zároveň slouží jako rybí přechod. Kóta pevného přelivu je 387,00 m n. m, tedy stejná jako kóta dna v korytě za přelivem. Běžná provozní hladina zdrže je 388,30 m n. m., zatímco maximální hladina zdrže je podle manipulačního řádu na kótě 388,50 m n. m. Podjezí bylo tvořeno 6 m dlouhým vývarem s hloubkou 0,8 m. V roce 2019 byl vývar rekonstruován, aby se vyhovělo hydraulickým podmínkám pro dostatečné tlumení kinetické energie vody přepadající přes jezový uzávěr.
Obr. 2. Jez Strakonice
Fig. 2. Strakonice weir
Fyzikální modely
Hydraulické jevy, proudění vody a hydraulické charakteristiky je možno zkoumat na skutečném vodním díle, nicméně z objektivních příčin je tento výzkum značně ztížen, a proto se přistupuje ke zkoumání na zmenšeném modelu v laboratoři. Počáteční, okrajové a limitující podmínky jsou dány rozměrovou, silovou a hmotnostní analýzou, jež vycházejí z podmínek zkoumání jevů na modelu pomocí Froudova zákona mechanické podobnosti [3].
Pro měření ve vodohospodářské laboratoři byly postaveny dva fyzikální modely. První z modelů o šířce 0,4 m pro jez Strakonice, tvořený klapkou s násoskou, byl postaven v měřítku 1 : 7. Na tomto modelu byly měřeny hladiny a průtoky pro různé polohy klapky s vyšším ovlivněním dolní vodou, neboť rozdíl mezi výškou dna v nadjezí a podjezí je 0 m. Druhým modelem o šířce 0,52 m v měřítku 1 : 12,5 byl jez Doksany (obr. 3), na němž byly měřeny hladiny a průtoky pro mimořádné situace, kdy není funkční zavzdušňovací potrubí anebo kdy hladina ve zdrži přesahuje maximální provozní hladinu.

Obr. 3. Fyzikální model jezu Doksany
Fig. 3. Physical model of Doksany weir
V rámci tohoto modelu byly rovněž posuzovány navzájem různé typy rozražečů (typ RV.x a RM.x) z hlediska průtočné kapacity (obr. 4). Vzhledem k modelovým podmínkám však nebylo možné určit vliv na součinitel přepadu. Přepočet jednotlivých charakteristik z fyzikálních modelů na skutečná vodní díla lze provést pomocí vzorců:
- měřítko délek ML
- měřítko rychlostí Mv = ML1/2
- měřítko průtoků MQ = ML5/2 [3]
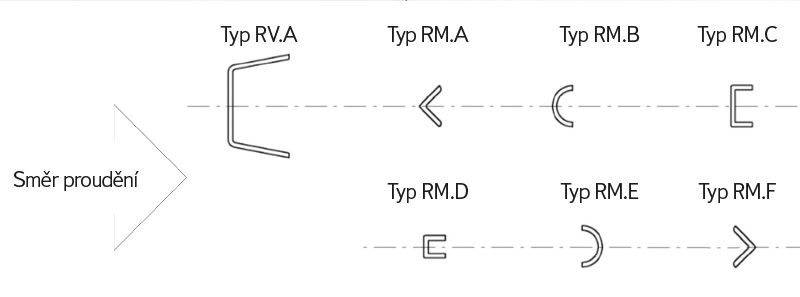
Obr. 4. Typy rozražečů
Fig. 4. Types of baffles
Matematický model
Matematický 3D model byl vytvořen pouze pro jez Doksany (obr. 5), přičemž byly zachovány stejné podmínky jako v případě fyzikálního modelu až na šířku modelu, kdy byla vymodelována pouze polovina jezového pole o délce 10 m. Výpočetní síť byla vytvořena v programu ICEM CFD a veškeré výpočty proběhly v programu Ansys CFX. V souvislosti s použitím funkce symetrie na modelu bylo pozdější verifikací zjištěno, že do modelu byla vnášena určitá chybovost, jež způsobovala vyšší průtočnou kapacitu [4, 5].
Cílem výběru výpočetní metody pro zjištění průtoku a proudění vody bylo pomocí CFD technologií určit nejistoty výpočtu. Výběr vhodné metody je klíčový pro minimalizaci nejistoty při matematickém modelování. Je nutné pečlivě vybrat metodu s ohledem na hydraulické chování a minimalizovat rizika při měření průtoku vodního díla [6].
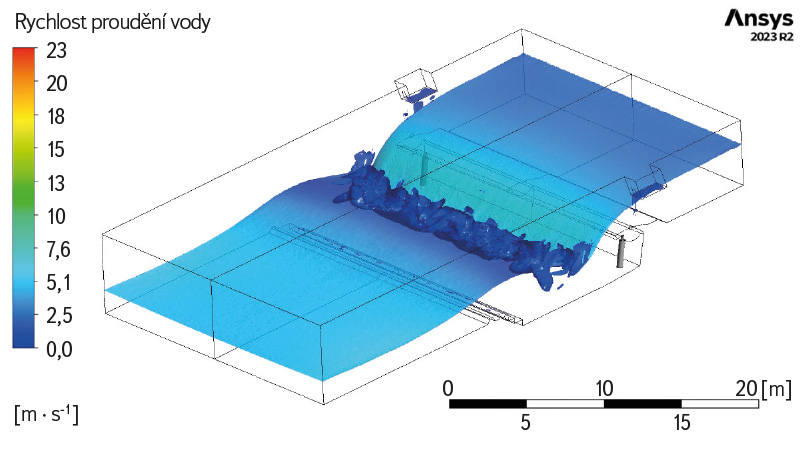
Obr. 5. Matematický model jezu Doksany
Fig. 5. Mathematical model of Doksany weir
Matematický model pohybu klapky
Při výpočtu průtoku přepadem přes klapku se v inženýrské praxi často odečítají výšky od klapky, jež se otáčí okolo nejnižší hrany, což však z hlediska skutečnosti není správné. Zavádí se tak do výpočtu chyba v přepadové výšce vlivem rozdílného sklopení klapkového uzávěru vůči skutečnosti, projevující se na konzumpční křivce, jež je důležitá z hlediska manipulací. Manipulace na vodním díle jsou poté nepřesné, což má za následek zhoršení operativního řízení vodních děl v rámci vodohospodářských soustav. Z tohoto důvodu bylo přistoupeno k odvození rovnic popisujících pohyb klapky se zavedením excentricity, která je mezi hradicím plechem a osou ložiska (obr. 6). Je nutné podotknout, že rovnice se týkají pohybu pro dutou klapku s poloměrem R = 2,25*H. Zároveň byly stanoveny rovnice pro pohyb rozražečů současně s klapkou. Veškeré rovnice včetně aplikace v rámci kalkulátorů jsou podrobně obsaženy v diplomové práci s názvem Hydraulická analýza klapkových uzávěrů a Jamborových prahů [7].
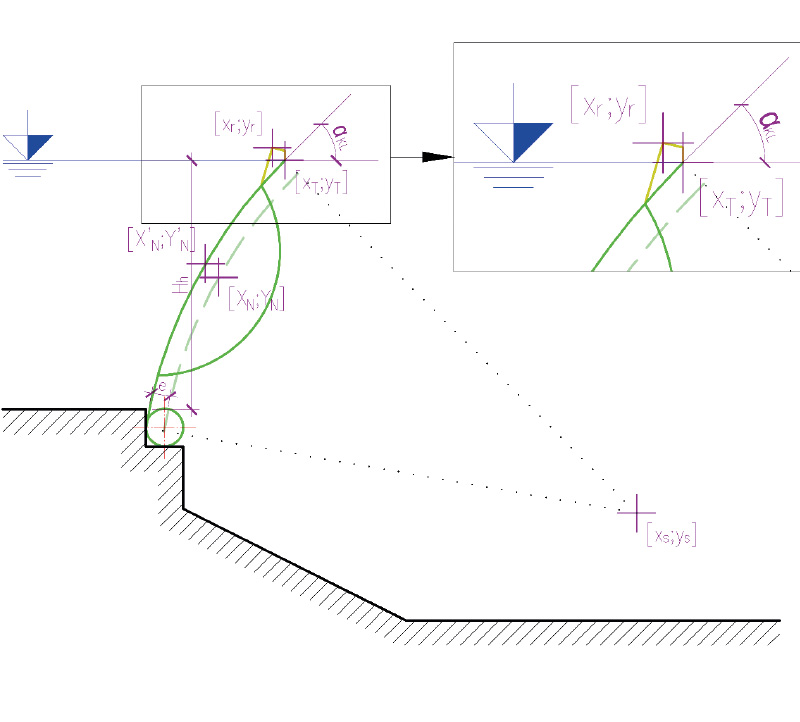
Obr. 6. Schéma klapkového uzávěru
Fig. 6. Diagram of a flap gate
VÝSLEDKY
Naměřená a vypočtená data modelů VD Doksany pro mimořádné situace byla vložena do již stávajícího grafu s křivkami J. Čábelky, v němž lze odečíst součinitel zatopeného přepadu µpσ (obr. 7). Tato data jsou zobrazena ve formě bodů z fyzikálního modelu (FM) a matematického modelu (MM) a nelze z nich vytvořit křivky, neboť každá naměřená hodnota odpovídá různému tlaku a zavzdušnění pod klapkou, jež jsou v praxi při mimořádných situacích neměřitelné. Z tohoto důvodu jsou hodnoty v grafu (obr. 7) pro praktickou aplikaci rozděleny podle stupně zatopení dolní vodou, poněvadž tento stupeň hraje významnější roli při použití ve výpočtech na dalších vodních dílech.
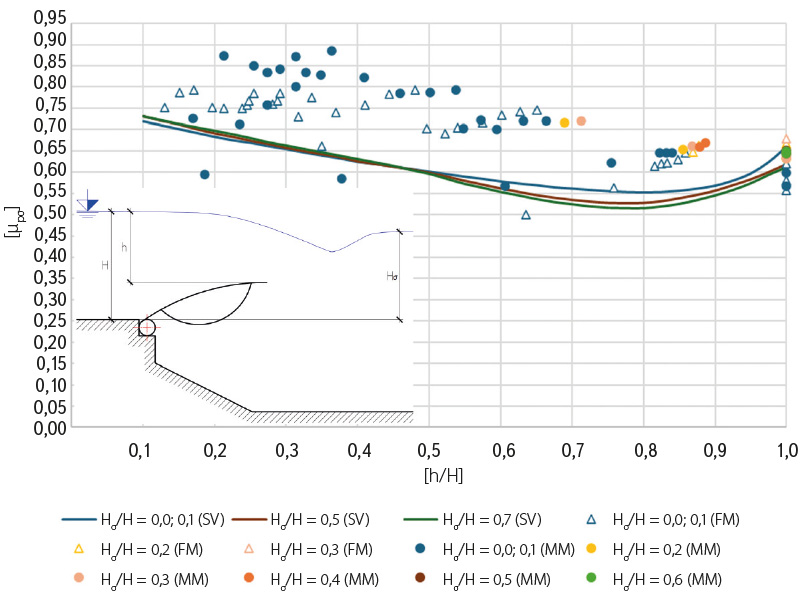
Obr. 7. Graf součinitele zatopeného přepadu pro mimořádné situace (nezavzdušněno)
Fig. 7. Graph of overfall coefficient for extraordinary situations (non-aerated)
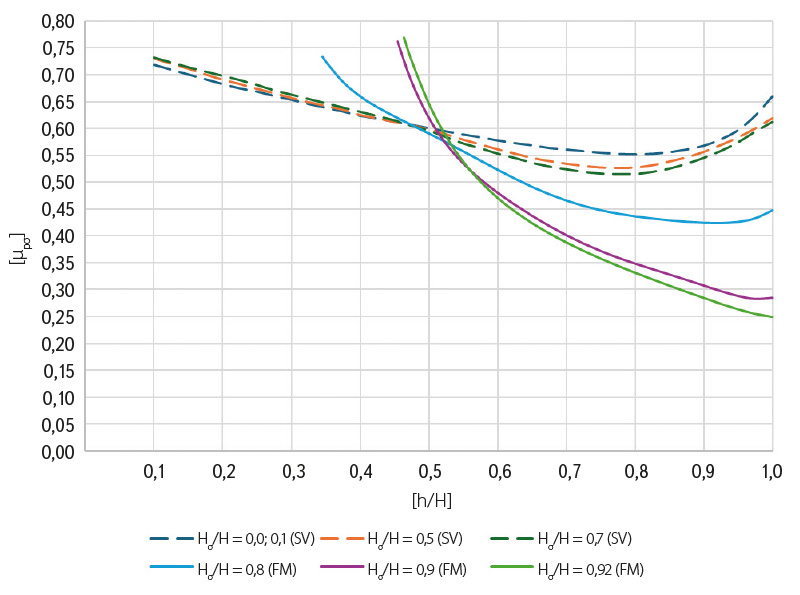
Obr. 8. Graf součinitele zatopeného přepadu pro běžné situace (zavzdušněno)
Fig. 8. Graph of overfall coefficient for ordinary situations (aerated)
Obdobně byla vložena data z měření na fyzikálním modelu VD Strakonice do téhož grafu J. Čábelky (obr. 8). Nicméně u těchto dat bylo možné proložení křivkami vzhledem k běžné situaci se zvýšenou hladinou dolní vody. Oproti výzkumu J. Čábelky, kdy poměr Hσ/H dosahoval hodnoty 0,7, bylo nyní možné dosáhnout na FM až hodnoty 0,92, což pomůže při výpočtu konzumpčních křivek na dalších vodních dílech, jakým je např. VD Klášterec na řece Ohři. Užití součinitele zatopeného přepadu je patrné v rovnici přepadu:
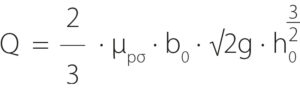
kde:
Q je průtok [m3 ∙ s-1]
µpσ součinitel zatopeného přepadu [-]
b0 účinná šířka přelivu [m]
g tíhové zrychlení [m ∙ s-2]
h0 energetická výška přepadu [m]
Výpočet energetické výšky přepadu se počítá prostřednictvím rovnice:
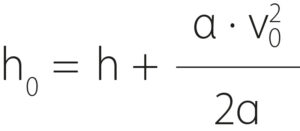
kde:
h0 je energetická výška přepadu [m]
α Coriolisovo číslo [-]
v0 přítoková rychlost [m ∙ s-1]
g tíhové zrychlení [m ∙ s-2]
Pro pochopení odečítání součinitele zatopeného přepadu µpσ je důležité znát parametry, jimiž se odečítá:
h je výška přepadu
H výška od koruny pevného jezu k hladině v nadjezí
Hσ výška od koruny pevného jezu k hladině dolní vody
Při zkoumání na klapkových uzávěrech vzešla z praxe otázka na podobnost hydraulického chování klapkového uzávěru a Jamborova prahu, přičemž objektem zájmu byla taková poloha klapky, jež by tuto konfiguraci splňovala. Na základě výzkumu J. Čábelky na klapkových uzávěrech a V. Laca [1] na Jamborových prazích bylo vyhodnoceno, že ke shodnému hydraulickému chování klapkového uzávěru dochází při úplném sklopení klapky anebo při zdvižení o cca 5 cm oproti plně sklopené klapce při různé výšce prahu p (obr. 9).
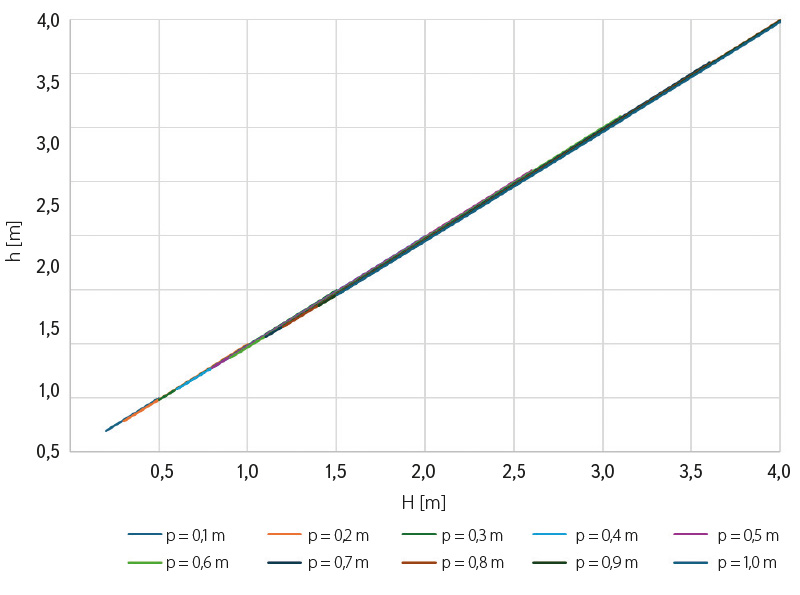
Obr. 9. Graf závislosti klapkového uzávěru a Jamborova prahu
Fig. 9. Graph of dependence of a flap gate and Jambor sill
Výzkumem klapkového uzávěru s přidanými velkými rozražeči a výměnnými malými rozražeči bylo docíleno stanovení ideálních typů rozražečů pro použití na skutečných vodních dílech (obr. 11), kde pomáhají při kmitání klapkového uzávěru při malých průtocích. Ideálními tvary rozražečů jsou profil L (typ RM.A) a půlkruh (typ RM.B), přičemž vrcholová hrana musí směřovat proti směru proudění vody. Rozražeče byly na fyzikálním modelu klapky rozvrženy v pořadí 1× RM.x, 1× RV.A, 2× RM.x, 1× RV.A, 2× RM.x, 1× RV.A, 1× RM.x, kdy osová vzdálenost mezi rozražeči RM.x byla 52 mm a mezi RV.A a RM.x 60 mm. Osová vzdálenost na modelu mezi rozražeči RV.A v případě bez kombinace
s RM.x činila 172 mm. Rozměry samotných rozražečů byly převzaty nebo sjednoceny dle klapkového uzávěru na VD Doksany. V rámci pozorování na modelu byly sledovány – nikoli měřeny – účinné šířky přepadu při nižších průtocích, přičemž pro kombinace rozražečů RV.A s RM.A byly monitorovány jednotlivé vodní paprsky přepadající přes klapku, zatímco u kombinací rozražečů RV.A s RM.B nebo RM.C nebo RM.D bylo pozorováno sjednocení vodních paprsků na krajích klapkového uzávěru. V případě kombinace rozražečů RV.A s RM.E či RM.F se vodní paprsek sjednotil pro celou osovou vzdálenost mezi rozražeči RV.A, tudíž vliv zúžení účinné šířky přepadu okolo rozražečů RM.E či RM.F nebyl patrný [7].
DISKUZE
Výsledky součinitele zatopeného přepadu pro mimořádné situace (obr. 7) poukazují na fakt, že při různě velkém zatopení zavzdušňovacího potrubí dochází ke zvýšení průtočnosti, přičemž z grafu lze vyčíst rozkolísanost výsledků. Tato rozkolísanost byla způsobena vlivem nestabilních tlaků, resp. podtlaků, které v praxi nesmějí nastat, neboť rozkmitávají konstrukci, což vede k jejímu následnému poškození. Vzhledem ke skutečnosti, že procentuální velikost zatopení zavzdušňovacího potrubí nelze při mimořádné situaci přímo na vodním díle naměřit, je zároveň možné takto naměřené a vypočtené hodnoty z modelů použít i pro další aplikace, avšak je nutno do dalších výpočtů zahrnout i rozptyl hodnot součinitele zatopeného přepadu.
V případě součinitele zatopeného přepadu pro běžné situace (obr. 8) při větším sklopení klapky a zároveň vyšším stupni zatopení lze pozorovat též vyšší hodnoty součinitele, což může být způsobeno též podtlaky jako v předchozím případě, a to i přes funkční zavzdušňovací potrubí. Nicméně se vzrůstající přepadovou výškou a s vyšším poklopením klapky hodnoty součinitele zatopeného přepadu v grafu ukazují vliv funkčního zavzdušňovacího potrubí, kdy hodnoty tohoto součinitele jsou znatelně nižší než při malém vlivu zatopení dolní vody. Potvrzení této teze lze očekávat po přepočítání konzumpčních křivek na VD Klášterec pracovníky státního podniku Povodí Ohře, kdy ověřením budou výsledky vodohospodářské bilance mezi profily před a za tímto vodním dílem.
V souvislosti s výše uvedenými výroky v návaznosti na graf závislosti klapkového uzávěru a Jamborova prahu (obr. 9) je možné potvrdit hodnoty v tomto grafu. Zároveň v grafu procentuálních odchylek klapkového uzávěru a Jamborova prahu (obr. 10) lze konkrétně vyčíst procentuální odchylku pro různá H, kdy tento graf potvrzuje shodné hydraulické chování klapkového uzávěru i při mírném zdvižení klapky o cca 5 cm oproti plně sklopené klapce při různé výšce prahu p. Pro lepší pochopení propojení obou grafů (obr. 9 a 10) lze např. odečíst z grafu (obr. 9) pro výšku H = 2 m, tj. od koruny pevného jezu k hladině v nadjezí, hodnotu výšky přepadu h mezi 0 až 5 cm, kdy s vyšší výškou prahu p vzrůstá jak výška přepadu, tak procentuální odchylka.
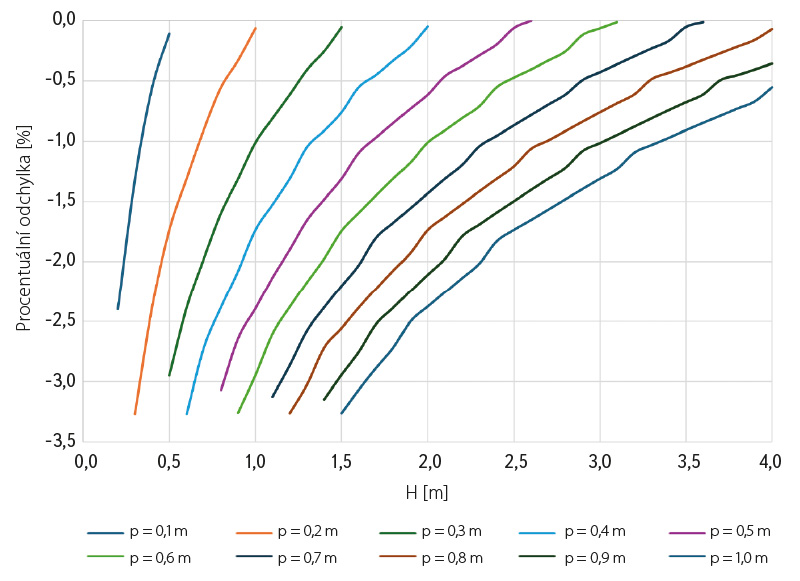
Obr. 10. Graf procentuální odchylky klapkového uzávěru a Jamborova prahu
Fig. 10. Graph of percentage deviation of a flap gate and Jambor sill
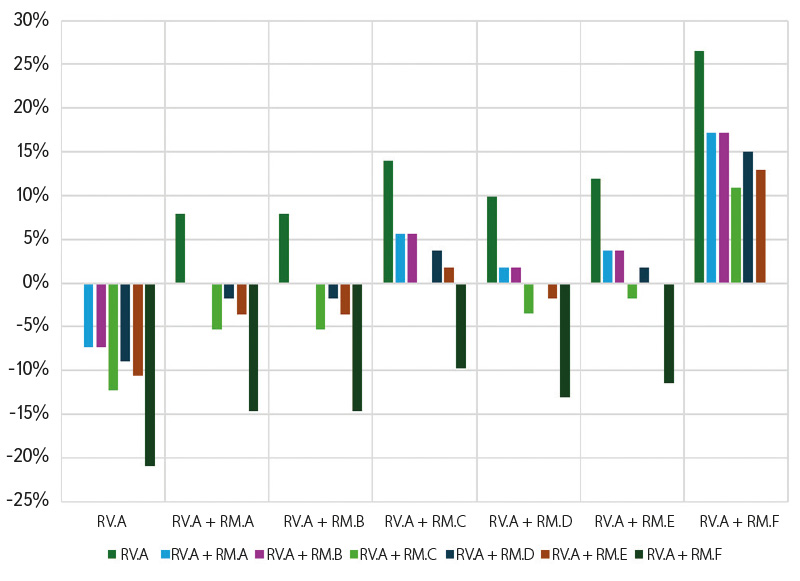
Obr. 11. Graf porovnání typů rozražečů
Fig. 11. Graph comparing types of baffles
Na základě porovnání typů rozražečů musíme dojít ke kritickému názoru, že stanovování součinitele přepadu pro různé geometrie rozražečů je pro praktické použití vlastně bezpředmětné. Nicméně výzkumem hydraulického chování právě těchto rozražečů byla pro další aplikace vyhodnocena ta nejlepší geometrie rozražeče, který plní svoji funkci a zároveň nesnižuje průtočnou kapacitu. Graf porovnání typů rozražečů (obr. 11) zobrazuje porovnání rozražečů z ukázky typů rozražečů (obr. 4), kdy graf lze číst jako porovnání, o kolik jsou horší varianty rozražečů ve sloupcích dle legendy oproti samotnému sloupci daného rozražeče, tzn. že např. v prvním sloupci rozražeče RV.A jsou všechny sloupce dle legendy s kombinacemi rozražečů RV.A + RM.A až RM.F v záporných procentech, poněvadž tyto kombinace rozražečů snižují průtočnou kapacitu celého klapkového uzávěru.
ZÁVĚRY
Výsledky výše popsaného výzkumu přinášejí nové poznatky o různých stavech a situacích na klapkových jezech. Použitím fyzikálních a matematických modelů bylo možné naměřit a dopočítat chybějící data v předchozích výzkumech, díky čemuž je nyní možné nové poznatky využít v inženýrské praxi. Vzhledem k faktu, že dutá klapka je nejpoužívanějším typem hradicího uzávěru na jezech a přehradách v ČR a na Slovensku, je díky tomuto výzkumu možno zpřesnit konzumpční křivky ve stávajících manipulačních řádech a opravit hodnoty v automatizovaných řídicích systémech vodních děl, čímž se zvýší bezpečnost vodního díla a zlepší se manipulace v rámci vodohospodářské soustavy.
U vodních děl s osazenými dutými klapkami s geometrií navrženou J. Čábelkou, tedy R = 2,25H, mohou být využity rovnice matematického popisu pohybu klapky se zavedenou excentricitou, díky čemuž se zjednoduší výpočetní postupy a zanedbají se chyby při odečítání hodnot z výkresové dokumentace. Tento inovativní přístup představuje praktický přínos při návrhu i následném opětovném posuzování hydraulických, statických a dynamických charakteristik. Současně při problematice kmitání klapkového uzávěru vlivem dynamického zatížení vodou je možné díky tomuto výzkumu použít vhodný typ rozražeče jako tlumícího prvku, který prodlouží životnost konstrukce a sníží negativní účinky při běžných, ale i mimořádných situacích.
Důležité je však zmínit, že neprozkoumanou oblastí grafu součinitele zatopeného přepadu dle J. Čábelky je interval poměru výšky přepadu k výšce hladiny h/H pro hodnoty menší než 0,1, pro jehož stanovení by bylo nutné mít k dispozici větší fyzikální model než doposud.
Poděkování
Příspěvek vznikl za podpory grantu ČVUT v Praze SGS25/084/OHK1/2T/11 „Kombinovaný výzkum proudění vody na hydrotechnických stavbách“.
Příspěvek prošel recenzním řízením.

