Souhrn
Hydraulické výpočty proudění vody v korytech vodních toků a záplavových územích se v současné inženýrské praxi provádějí primárně s použitím 1D, 2D a spřažených 1D/2D numerických modelů. Matematický model je v případě zmiňované 2D schematizace obvykle založen na tzv. rovnicích proudění v mělkém proudu (shallow water equations), přičemž k matematickému popisu turbulentního proudění se zde využívají tzv. turbulentní modely s různým pojetím modelování turbulence. V našich podmínkách je pro účely hydraulických výpočtů poměrně rozšířené programové vybavení HEC-RAS, které využívá turbulentního modelu založeného na Boussinesqově aproximaci. Cílem příspěvku je prezentace postupů a závěrů citlivostní analýzy, jež zohledňuje vliv vstupních parametrů uvedeného turbulentního modelu na výsledky hydraulických výpočtů v případě použití 2D, respektive spřaženého 1D/2D modelu. Součástí analýz je rovněž ověření možného ovlivnění výsledků změnami dalších parametrů výpočtu, mezi které patří např. zavedení zjednodušeného řešení rovnic proudění v mělkém proudu aproximací difuzní vlnou nebo způsob prostorové diskretizace řešené náhradní oblasti. K ověřovacím výpočtům byl vybrán jednak fiktivní úsek prizmatického koryta lichoběžníkového průřezu a dále reálný úsek koryta toku Svratka na území města Brna v délce cca 2,6 km. Účelem předkládaného příspěvku je především poskytnout potenciálním uživatelům 2D numerických modelů, založených na rovnicích mělkého proudu, základní představu o nejistotách ve výsledcích hydraulických výpočtů, vyplývajících z volby vybraných vstupních parametrů.
Úvod
Pro účely hydraulických výpočtů proudění vody v korytech toků a záplavových územích se v současnosti v inženýrské praxi využívají primárně 1D, 2D a spřažené 1D/2D numerické modely. Uvedený typ hydraulických výpočtů zpravidla představuje časově – a tedy i finančně – náročnou proceduru, která je zatížena řadou nejistot. Jako jeden z podstatných zdrojů nejistot lze označit volbu vhodného hydrodynamického modelu k provedení hydraulických výpočtů a s tím související způsob schematizace řešené oblasti. Volba dimenze modelu spolu s dalšími vstupními parametry může mít podstatný vliv na výsledky výpočtů. Zatímco 2D modely vycházejí z předpokladu dvourozměrného (2D) proudění vody na celé řešené náhradní oblasti, spřažené 1D/2D modely uvažují v dílčích částech řešené oblasti s jednorozměrným (1D) přístupem [2–9]. Obvyklá je schematizace samotného vodního toku v rozsahu břehových hran pomocí 1D modelu a přilehlého záplavového území 2D modelem. Hlavním přínosem použití spřažených 1D/2D modelů je zejména snadnější hydraulické řešení objektů v zájmové oblasti (např. mosty, propustky, jezy) a dále menší nároky na podklady zachycující morfologii koryta řešených vodních toků. V případě 1D modelu lze koryto toku schematizovat soustavou příčných řezů, zatímco pro 2D model je nezbytné zajistit kompletní digitální model reliéfu koryta toku. Nevýhodou použití spřažených 1D/2D modelů oproti 2D modelům mohou být např. přijatá zjednodušení hydraulických jevů v místech propojení mezi 1D a 2D oblastmi a možná větší časová náročnost prováděných výpočtů. Obecně je problematice srovnání 1D, 2D a 1D/2D hydrodynamických modelů věnována řada publikací, viz např. [10–17].
Zmiňované 2D numerické modely jsou obvykle založeny na matematickém modelu zahrnujícím tzv. rovnice proudění v mělkém proudu (shallow water equations) [18], jež v různé míře umožňují rovněž zohlednění turbulence. K matematickému popisu turbulentního proudění se využívají tzv. turbulentní modely s různým pojetím modelování turbulence [1]. V našich podmínkách je pro účely hydraulických výpočtů poměrně rozšířené programové vybavení HEC-RAS, které v rámci 2D schematizace využívá turbulentního modelu založeného na Boussinesqově aproximaci [18]. Jeho podstatou je zavedení tzv. turbulentní viskozity. Pro její výpočet je však nezbytná specifikace bezrozměrného koeficientu, jenž je závislý na charakteru proudění a může nabývat hodnot v poměrně širokém rozpětí [18–20].
Cílem příspěvku je prezentace výsledků citlivostní analýzy zohledňující vliv uvedeného vstupního parametru turbulentního modelu na výsledky hydraulických výpočtů v případě použití 2D schematizace, respektive při použití spřaženého 1D/2D modelu. Součástí analýz je rovněž ověření možného ovlivnění výsledků změnami dalších parametrů výpočtu, mezi něž patří např. zavedení zjednodušeného řešení rovnic proudění v mělkém proudu aproximací difuzní vlnou nebo způsob prostorové diskretizace řešené náhradní oblasti. K ověřovacím výpočtům byl vybrán jednak fiktivní úsek prizmatického koryta lichoběžníkového průřezu a dále reálný úsek koryta toku Svratka na území města Brna v délce cca 2,6 km. Předkládaný příspěvek si neklade za cíl detailní teoretický rozbor daného problému. Jeho účelem je především poskytnout uživatelům 2D numerických modelů, založených na rovnicích mělkého proudu, základní představu o nejistotách ve výsledcích hydraulických výpočtů vyplývajících z volby vybraných vstupních parametrů.
Metoda citlivostní analýzy
Citlivostní analýza vlivu bezrozměrného koeficientu pro výpočet turbulentní viskozity na výsledky hydraulických výpočtů proudění vody v korytech toků a záplavových územích spočívá v realizaci a následné analýze řady variantních výpočtů s použitím 2D, respektive spřaženého 1D/2D numerického modelu. Pro tyto účely bylo zvoleno poměrně rozšířené programové vybavení HEC-RAS, které je založeno na matematickém modelu dvourozměrného (2D) proudění kapaliny o malé hloubce s volnou hladinou, tj. na tzv. rovnicích proudění v mělkém proudu (FM). Matematický model dále umožňuje výpočty s použitím zjednodušené formy rovnic mělkého proudu bez použití turbulentního modelu, označované jako aproximace difuzní vlnou (DW). Pro srovnání byl rovněž využit matematický model s jednorozměrnou (1D) schematizací. Podrobný teoretický popis zmiňovaných matematických modelů lze nalézt např. v literatuře [18]. Konkrétní uživatelské nastavení parametrů v programu HEC-RAS lze provést s použitím příručky [22] (viz klíčová slova „Eddy Viscosity Transverse Mixing Coefficient“, „Full Momentum Equation“ a „Diffusion Wave“).
Jednotlivé řešené varianty se v rámci citlivostní analýzy lišily použitím různých hodnot bezrozměrného koeficientu D, nezbytného pro výpočet turbulentní viskozity, která je podstatou turbulentního modelu využívajícího Boussinesqovu aproximaci. Sledovanou veličinou byla ve všech případech vypočtená úroveň hladiny v ose řešených koryt toků. Zmiňovanou turbulentní (tzv. „eddy“) viskozitu vt, vstupující do řešení rovnic proudění v mělkém proudu (FM), lze vyjádřit vztahem [18]:

kde D je bezrozměrný koeficient pro výpočet turbulentní viskozity a smyková rychlost definovaná jako:
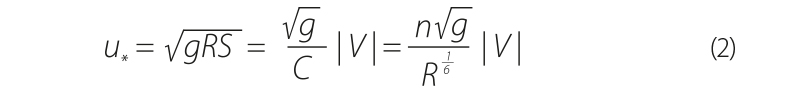
kde R je hydraulický poloměr, g tíhové zrychlení, S sklon čáry energie, C Chézyho rychlostní součinitel, |V| střední svislicová rychlost a n Manningův drsnostní součinitel. Pro hydraulické výpočty v programu HEC-RAS udává Brunner [18] orientační rozsahy hodnot bezrozměrného koeficientu D pro výpočet turbulentní viskozity uvedené v tab. 1.
Tab. 1. Hodnoty bezrozměrného koeficientu D pro výpočet turbulentní viskozity dle [18]
Tab. 1. Values of eddie viscosity transverse mixing coefficient D [18]

Citlivostní analýza byla provedena na dvou typech modelů, které jsou v dalším textu označeny písmeny A, B. Model A byl koncipován s ohledem na eliminaci dalších možných vlivů na výsledky výpočtů (nerovnoměrnost rychlostního pole, náhlé kontrakce při změnách tvaru příčných profilů apod.). Z tohoto důvodu bylo pro citlivostní analýzu zvoleno prizmatické koryto lichoběžníkového průřezu, jehož hlavní parametry jsou patrné z obr. 1 a tab. 2. Pro účely simulace odlehčování části průtoku do inundačního území bylo do modelu A začleněno rovněž pravobřežní lokální snížení břehové hrany o 0,3 m v délce 100 m, nacházející se uprostřed délky řešeného úseku koryta (viz obr. 1 a 6). Za takto vytvořenou přelivnou hranou byl zaveden předpoklad volného odtoku vody.
Tab. 2. Model A – základní parametry koryta
Tab. 2. Model A – river reach basic parameters

Pro výše popsaný model A byla následně provedena citlivostní analýza spočívající ve variantních výpočtech A.1 až A.4. Nastavení jednotlivých variant (viz tab. 3) bylo voleno tak, aby byl vždy jeden z testovaných vstupních parametrů modelu zadán jako konstantní a druhý s proměnlivými hodnotami (viz sloupce výpočetní síť a koeficient turbulence D v tab. 3). Zároveň ve všech řešených va- riantách proběhlo ověření vlivu použitého matematického modelu (viz sloupec model).
Tab. 3. Model A – základní parametry řešených variant výpočtů
Tab. 3. Model A – basic parameters of solved calculation variants

Výsledky 1D modelu byly určeny pouze k orientačnímu srovnání s 2D modely a nebyly předmětem citlivostní analýzy. Zvolená velikost elementů výpočetní sítě odpovídala rozměrům koryta v příčném profilu dle obr. 1. Rozměr elementů 18 m postihoval celou šířku koryta, rozměr 6 m odpovídal dělení profilu na svahy a dno, rozměry elementů 1 m, 0,5 m a 0,25 m sloužily k ověření vlivu jemnějšího dělení oblasti. Model B zachycuje reálný úsek vodního toku Svratky (viz obr. 2) cca mezi km 50,2 (jez Kamenný mlýn) až km 52,8 (jez Komín).
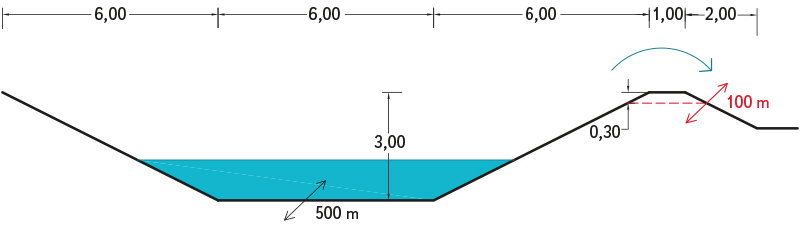
Obr. 1. Model A – příčný profil koryta toku (přeliv je ve funkci pouze u varianty A.4 dle tab. 3)
Fig. 1. Model A – river reach cross section (the overflow is functional only for variant A.4 according to tab. 3)
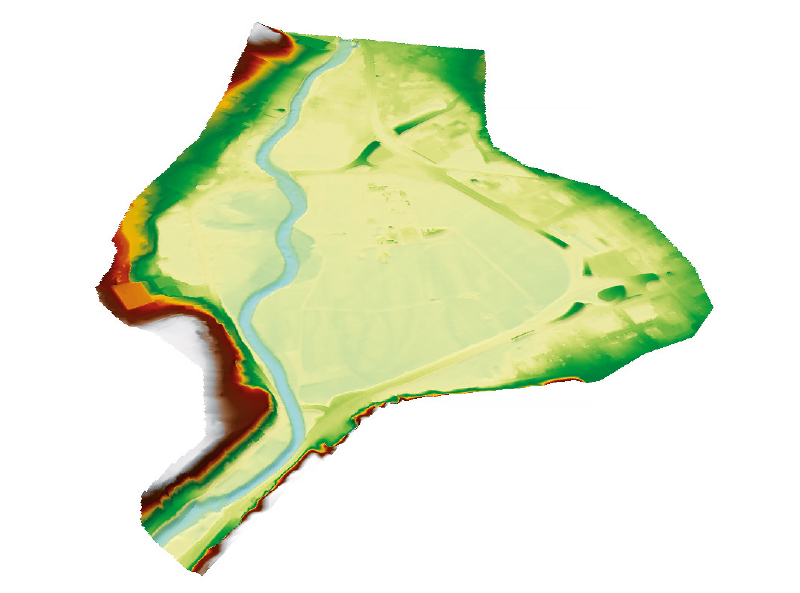
Obr. 2. Situace modelu řeky Svratky v úseku km 50,2 až km 52,8
Fig. 2. Situation of the Svratka river model in the section of km 50.2 to km 52.8
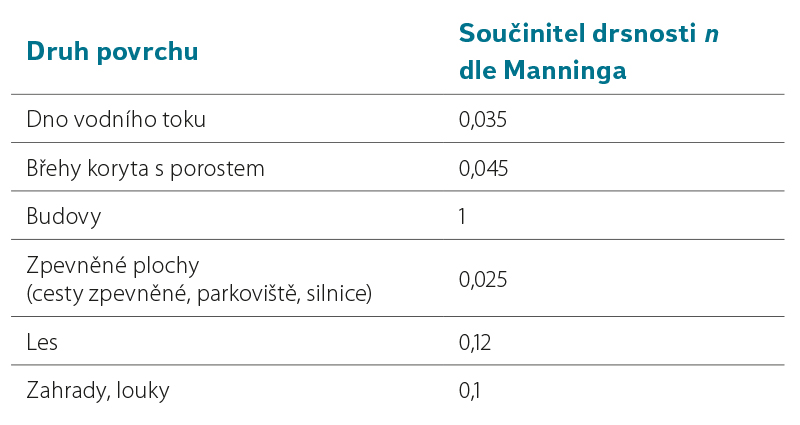
Pro řešenou lokalitu byl připraven digitální model terénu sestavený na základě dat z digitálního modelu reliéfu 5. generace (DMR 5G) [21] a ze sonarového zaměření dna koryta toku Svratka. Dále bylo provedeno dílčí geodetické zaměření vybraných terénních hran metodou GPS – RTK (např. břehové hrany, zemní tělesa komunikací apod.). Rozložení drsností povrchu v zájmovém území bylo stanoveno odborným odhadem na základě místních šetření a mapových podkladů ZABAGED [21]. Konkrétní použité hodnoty součinitelů drsností n dle Manninga jsou uvedeny v tab. 4.
Tab. 4. Součinitelé drsnosti povrchu n dle Manninga pro model B
Tab. 4. Manning roughness coefficients n for model B
Samotné sestavení modelu v programu HEC-RAS proběhlo s použitím aplikace RAS Mapper. Do modelu proudění byl připojen digitální model terénu a vrstva drsností povrchu. Pro zadanou oblast modelu proudění byly doplněny významné linie (břehové linie, terénní zlomy, příčné objekty v korytě). Výpočetní síť řešené náhradní oblasti byla tvořena elementy ve tvaru hexagonu s rozměry cca 8 × 8 m a s lokálním zjemněním v okolí významných linií. Hexagonální elementy umožňují, oproti čtvercovým elementům použitým v případě modelu A, snadnější tvorbu výpočtových sítí s nepravidelnými hranicemi náhradních oblastí, popř. s požadavky lokální změny velikostí elementů. Výpočetní síť sestávala z celkového počtu 80 200 elementů. Dolní okrajová podmínka byla zadána měrnou křivkou jezu Kamenný mlýn ve staničení km 50,2, horní okrajová podmínka byla zadána hodnotou průtoku (viz tab. 5). Vytvořený 2D model byl následně upraven dle jednotlivých řešených variant výpočtu (viz tab. 5), tj. byly zadávány různé hodnoty bezrozměrného koeficientu D pro výpočet turbulentní viskozity, použita aproximace difuzní vlnou apod.
Za účelem srovnání výsledků výpočtů byl vytvořen rovněž 1D numerický model koryta toku Svratka v zájmovém úseku tak, aby s maximální mírou respektoval parametry 2D modelu. V případě 1D modelu byla provedena schematizace geometrie koryta toku zadáním osy a příčných řezů ve vzdálenostech 10 m.
Citlivostní analýza byla provedena nad výsledky výpočtů ve variantách B.1 a B.2 s parametry uvedenými v tab. 5. Ve variantě B.1 byla zvolena hodnota kulminačního průtoku Q5, který přibližně odpovídal kapacitě řešeného úseku koryta. Při průtoku Q20, použitém ve variantě B.2, již docházelo v malém rozsahu k rozlivům do přilehlého území. Takto vzniklá inundační území však nebyla průtočná a případné změny průtoku podél zájmového úseku toku lze považovat za zanedbatelné.
Tab. 5. Model B – základní parametry řešených variant výpočtů
Tab. 5. Model B – basic parameters of solved calculation variants

Výsledky citlivostní analýzy
Výsledky řešených variant A.1 až A.4 pro model A, prizmatického lichoběžníkového koryta, jsou patrné z obr. 3 až 6. V případě citlivostní analýzy vlivu prostorové diskretizace bez zohlednění turbulence (viz varianta A.1 na obr. 3) je patrné, že za předpokladu shodné velikosti elementů výpočetní sítě jsou rozdíly mezi modely 2D (FM) a 2D (DW) minimální. V porovnání s 1D modelem narůstají rozdíly ve vypočtených hloubkách vody se zmenšující se velikostí výpočtových elementů. Jako hraniční je možné označit rozměr elementu cca 1 m, od kterého má již další zjemňování výpočetní sítě nepatrný vliv.
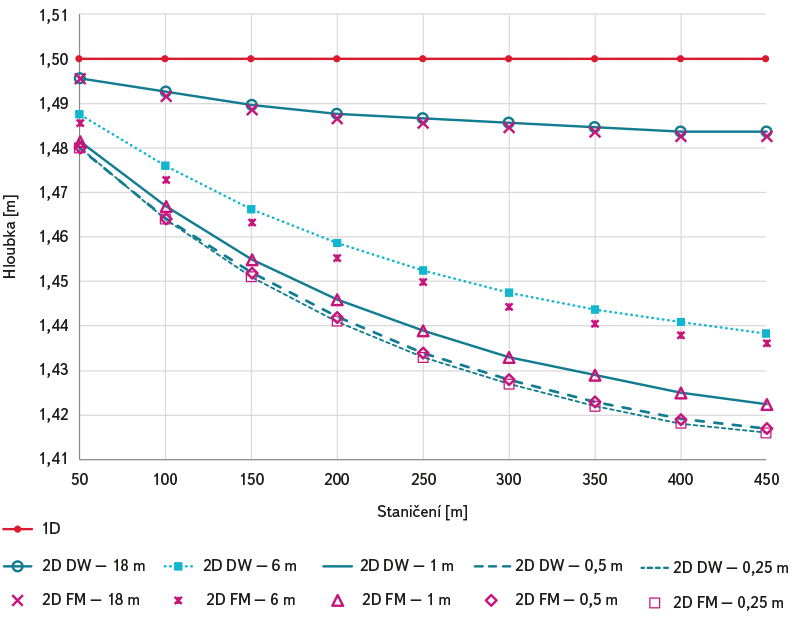
Obr. 3. Varianta A.1 – výsledky citlivostní analýzy vlivu prostorové diskretizace bez zohlednění turbulence (model 2D DW nebo 2D FM s D = 0)
Fig. 3. Variant A.1 – results of sensitivity analysis of the influence of spatial discretization without taking into account turbulence (model 2D DW or 2D FM with D = 0)
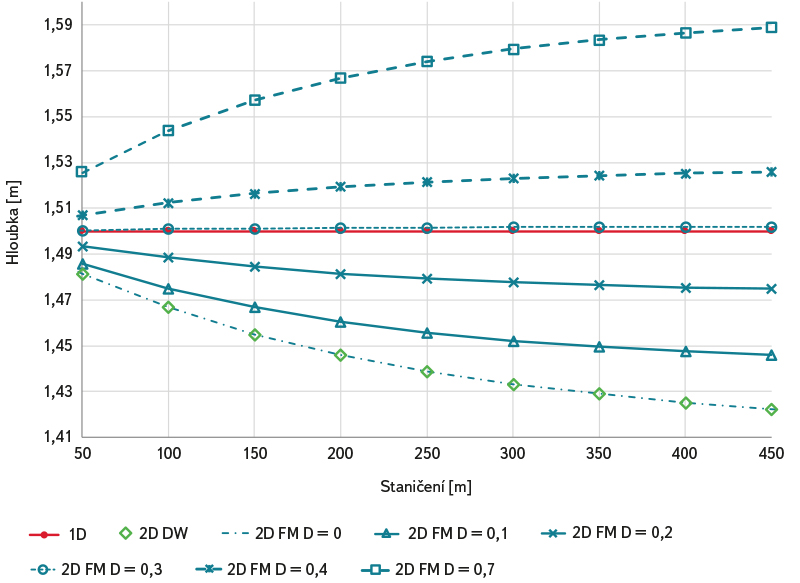
Obr. 4. Varianta A.2 – výsledky citlivostní analýzy vlivu parametrů turbulentního modelu (konstantní velikost elementů 1 m)
Fig. 4. Variant A.2 – results of sensitivity analysis of the influence of turbulence model parameters (constant size of elements 1 m)
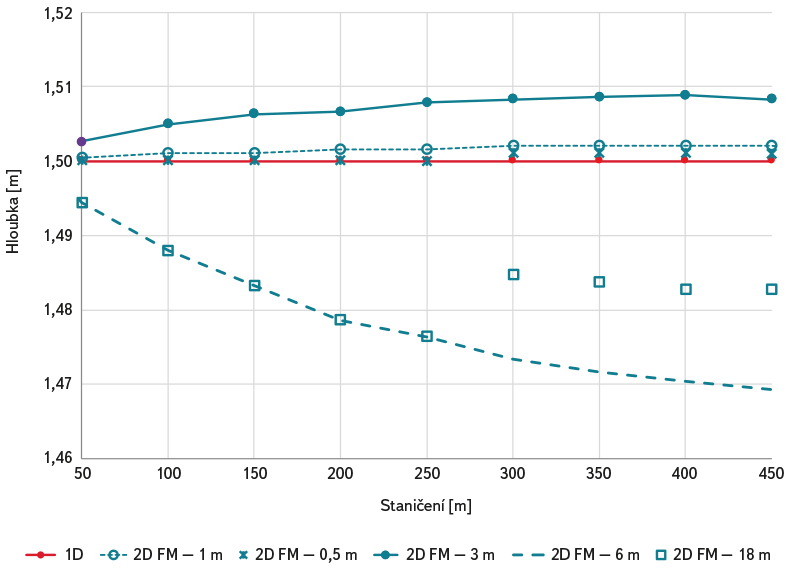
Obr. 5. Varianta A.3 – výsledky citlivostní analýzy vlivu volby prostorové diskretizace při konstantních parametrech turbulentního modelu (D = 0,3)
Fig. 5. Variant A.3 – results of sensitivity analysis of the influence of the choice of spatial discretization at constant parameters of the turbulence model (D = 0,3)
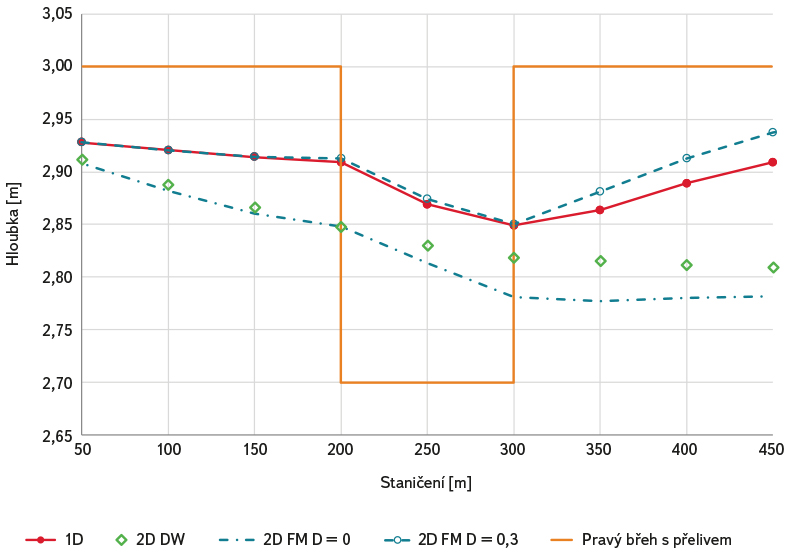
Obr. 6. Varianta A.4 – výsledky citlivostní analýzy vlivu parametrů turbulentního modelu při bočním odlehčení průtoků z koryta (konstantní velikost elementů 1 m)
Fig. 6. Variant A.4 – results of sensitivity analysis of the influence of turbulence model parameters during lateral overflow from the river reach (constant size of elements 1 m)
Z výsledků citlivostní analýzy vlivu parametru turbulence při konstantních rozměrech výpočtové sítě s velikostí elementu 1 m (viz varianta A.2 na obr. 4) je patrné, že výsledkům 1D modelu se nejvíce blíží hloubky vody vypočtené pomocí modelu 2D (FM) s koeficientem D = 0,30. Zjištěná hodnota D = 0,30 je na hranici doporučovaného rozpětí hodnot dle tab. 1 pro zvolený typ přímého prizmatického koryta. Z obr. 4 je rovněž jasně patrný logický trend zvyšování úrovně hladiny, resp. hloubek vody v souvislosti s nárůstem hodnoty koeficientu D. Dolní obálku zjištěných hloubek vody naopak představují výsledky modelů 2D (FM) s D = 0 a 2D (DW), tj. bez zohlednění vlivu turbulence.
Citlivostní analýza vlivu zvolené prostorové diskretizace při uvažování konstantního koeficientu D = 0,30 (viz varianta A.3 na obr. 5) prokázala, že zvolená velikost elementů výpočetní sítě má při konstantní hodnotě koeficient D = 0,30 vliv na vypočtené úrovně hladin. Odchylky v tomto případě narůstají se zvětšující se velikostí elementu. Jako hraniční lze, obdobně jako ve variantě A.1, označit velikost elementu cca 1 m. Výsledky ve variantě A.4 na obr. 6 s pravobřežním odlehčením průtoku potvrzují skutečnosti zjištěné v předchozích variantách A.1 až A.3. Oproti variantám bez odlehčení je zde patrné ovlivnění úrovní hladin v úseku nad přelivem.
Výsledky ve variantách B.1 a B.2, provedené na reálném úseku koryta, v zásadě potvrzují základní skutečnosti zjištěné ve variantách A.1 až A.4 pro fiktivní prizmatické koryto. Z obr. 7 a 8 je patrný nezanedbatelný vliv bezrozměrného koeficientu D na úroveň hladiny při výpočtech s použitím modelu 2D (FM), tj. nárůst úrovně hladiny v souvislosti se zvyšováním hodnoty koeficientu D. Při vzájemném srovnání výsledků 2D (FM) a 1D modelu jsou oproti prizmatickému korytu (viz model A) patrné výrazně vyšší úrovně vypočtených hladin, a to i v případě doporučeného rozmezí hodnot koeficientu D dle tab. 1. Výsledky modelu 2D (DW) vykazují naopak úrovně hladin podstatně nižší, než je tomu u 1D modelu. U modelu B se ve srovnání s prizmatickým korytem v modelu A dále neprokázala shoda ve výsledcích výpočtů pomocí modelů 2D (FM) s D = 0 a 2D (DW), tj. bez uvažování vlivu turbulence.
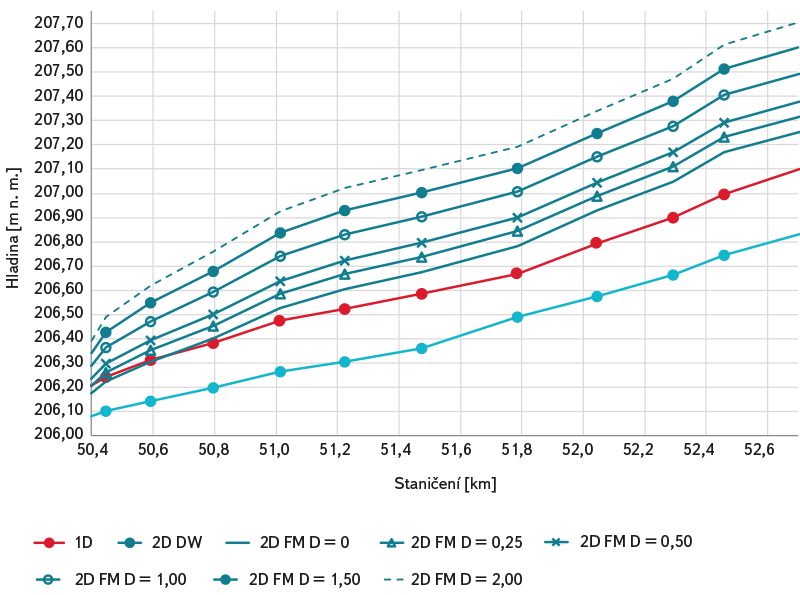
Obr. 7. Varianta B.1 – výsledky citlivostní analýzy vlivu bezrozměrného koeficientu D na úroveň hladiny při průtoku Q5
Fig. 7. Variant B.1 – results of sensitivity analysis of the influence of dimensionless
coefficient D on the water level at discharge Q5
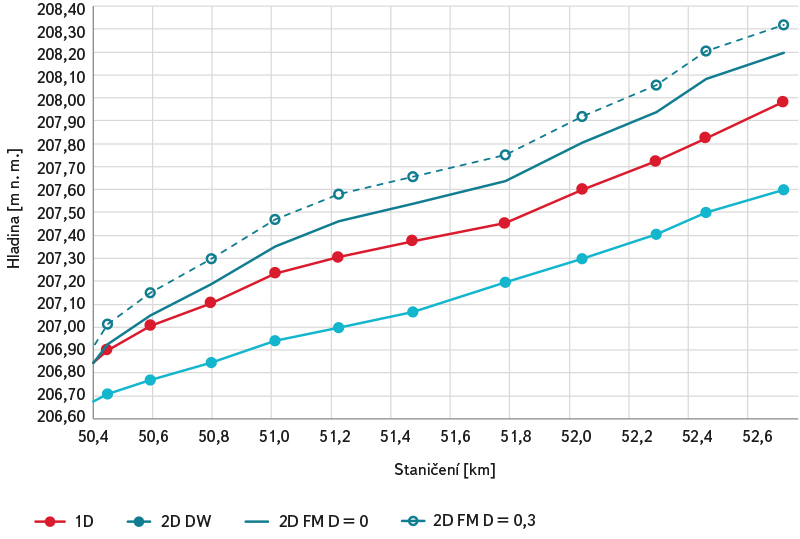
Obr. 8. Varianta B.2 – výsledky citlivostní analýzy vlivu bezrozměrného koeficientu D na úroveň hladiny při průtoku Q20
Fig. 8. Variant B.2 – results of sensitivity analysis of the influence of dimensionless
coefficient D on the water level at discharge Q20
Závěr a diskuze výsledků
Zohlednění vlivu turbulence při hydraulických výpočtech s použitím 2D, resp. spřažených 1D/2D numerických modelů s sebou většinou přináší zvýšenou časovou náročnost výpočtů, a to jak z hlediska podstatného prodloužení výpočetního času, tak po stránce vyšších nároků na kalibraci modelu. Provedenou citlivostní analýzou byla na modelových případech ověřena závislost vypočtených úrovní hladin na bezrozměrném koeficientu D pro výpočet turbulentní viskozity a související prostorové diskretizaci řešené náhradní oblasti. S ohledem na rozsah provedených analýz a celkovou teoretickou náročnost řešené problematiky lze předkládaný příspěvek chápat jako úvod do daného tématu. Dosažené výsledky poskytují potenciálním uživatelům orientační představu o míře nejistot vyplývajících z případného zohlednění, resp. zanedbání vlivu turbulence. Za stavu, kdy jsou v praxi obvykle značně omezené zdroje odpovídajících kalibračních údajů, představuje naznačený postup citlivostní analýzy vhodný způsob pro získání základní představy o míře nejistot, kterou jsou zatíženy výsledky výpočtů. Zjištěné skutečnosti rovněž nabízejí možnosti dalšího podrobnějšího výzkumu v dané oblasti. V této souvislosti lze zmínit např. otázku nejistot souvisejících s hydraulickým řešením oblastí, kde dochází k vybřežování vody z koryta toku do přilehlého záplavového území, resp. k jejímu zpětnému nátoku např. v důsledku přelévání ochranných hrází nebo překročení kapacity koryta.
Poděkování
Příspěvek vznikl za podpory projektu FAST-S-20-6305 „Nejistoty v hydraulickém posouzení transformačního účinku údolní nivy s použitím 2D a spřažených 1D/2D numerických modelů“.
Příspěvek prošel lektorským řízením.
