Souhrn
Odra River Alarm Modul (ORAM) bude součástí projektu NAVAROSO. V posledních dvaceti letech nejsou k dispozici žádné výsledky ze stopovacích pokusů české části řeky Odry. Z toho důvodu byly pro analýzu použity výsledky ze stopovacích pokusů na řece Svitavě. Tento článek je specificky zaměřen na analýzu pěti průnikových křivek. Nejlepší aproximace průnikové křivky ve všech pěti případech byla dána rovnicí (5) – Pearsonovým rozdělením III. typu. Počítá se s tím, že výsledky analýzy budou použity při tvorbě ORAM.

Úvod
Pro modelování šíření havarijního znečištění v tocích se obvykle používají 1D modely. Jako příklady možno uvést Rhine Alarm Model (RAM), Danube Basin Alarm Model (DBAM), Poplachový model Labe (ALAMO), v USA je to například model RiverSpill, v Rusku je možno jmenovat například model řeky Tura. Náš výzkumný ústav pracuje na projektu NAVAROSO. Jedná se o vývoj expertního informačního systému, jehož cílem je vytvoření a naplnění specializovaného databázového softwaru, umožňujícího rychlé poskytování křížově provázaných údajů o tocích, potenciálních znečišťovatelích a látkách, které mohou znečištění toků způsobit a tvorba verzí pro stacionární i mobilní zařízení (pro operační systémy Android, iOS a Windows Phone). Tato databáze bude doplněna modulem umožňujícím hrubý odhad šíření havarijního znečištění vodním tokem. Modul bude testován na řece Odře nad státní hranicí s Polskem pod názvem ORAM (Odra River Alarm Modul) a zaměří se jmenovitě na toky Odra, Olše, Ostravice, Opava a Lučina. Cílem tohoto článku je seznámit čtenáře s některými poznatky, které byly získány během přípravy tohoto modulu.
Metodika
Připravuje se modul umožňující odhady šíření havarijního znečištění v toku. V současné době je nedostatek podrobných údajů o vodních tocích, pro které má modul sloužit, proto se v první fázi modul omezí na metodu předběžných odhadů. Cílem je poskytovat správci toku, vodohospodářskému orgánu, hasičskému záchrannému sboru a dalším zainteresovaným složkám při řešení havarijních situací orientační informace o dobách doběhu čela mraku znečištění do jednotlivých profilů na toku. V případech, kdy bude k dispozici odhad množství uniklé znečišťující látky při okamžitém vnosu, umožní modul také odhad maximální koncentrace, která pravděpodobně bude dosažena ve zvoleném zájmovém profilu na toku. K předběžným odhadům dotokových dob budou použity empirické rovnice, které jsou výsledkem statistické analýzy velkého množství stopovacích pokusů uvedené v [1]. V budoucnu se počítá se zdokonalením tohoto modulu. To však předpokládá daleko vyšší nároky na přípravu vstupních dat týkajících se vodních toků (geometrie, hydrodynamika, …), dat pro modelování transportu látek (disperzní součinitele, konstanty kinetiky), apod. Rozsah podkladů potřebný pro takový model je uveden například v [2]. Současná příprava modulu se zaměřuje na tři na sebe navazující kroky. Prvním krokem je predikce dotokových dob, druhým predikce maximální koncentrace v zájmovém profilu a třetím krokem predikce rozdělení koncentrací během průchodu znečištění zájmovým profilem, jinými slovy predikce průnikové křivky v zájmovém profilu. Dotokové doby můžeme získat buď přímo měřením při stopovacích pokusech, nebo pomocí výpočtů. Výpočty mohou být buď hydrotechnické, nebo empirické. Empirické vzorce opírající se o hydrologické údaje a údaje ze stopovacích pokusů uvádí například Jobson [1]. Na dolním toku řeky Ostravice a v úseku Odry mezi ústím Ostravice a státní hranicí s Polskem lze dotokové doby odvodit z kontinuálního měření konduktivity a průtoků ve stanicích Slezská Ostrava a Bohumín a údajů o vypouštění slaných důlních vod. Problematika dotokových dob je poměrně rozsáhlá a není předmětem tohoto článku. Nejdůležitější dotokové doby jsou znázorněny na obr. 1. Dotoková doba je rozdíl mezi dvěma časy, kde t0 je čas okamžitého vnosu, tB je čas, ve kterém znečištění dorazí do zájmového profilu, tL je čas, ve kterém znečištění dosáhne 10 % maximální koncentrace v zájmovém profilu, tP je čas, ve kterém znečištění dosáhne maximální koncentrace v zájmovém profilu, tT je čas, ve kterém znečištění poklesne 10 % maximální koncentrace v zájmovém profilu, tE je čas ve kterém znečištění opustí zájmový profil a Cp je maximální koncentrace znečišťující látky dosažená během průchodu zájmovým profilem ve vzdálenosti x od místa vnosu. Zájmový profil je profil, ve kterém chceme znát maximální koncentraci. Protože časy tB a tE je velice obtížné určit, používají se v praxi při analýze výsledků stopovacích pokusů časy, ve kterých koncentrace dosáhne 10 % z maximální koncentrace, tyto časy jsou označeny tL a tT.
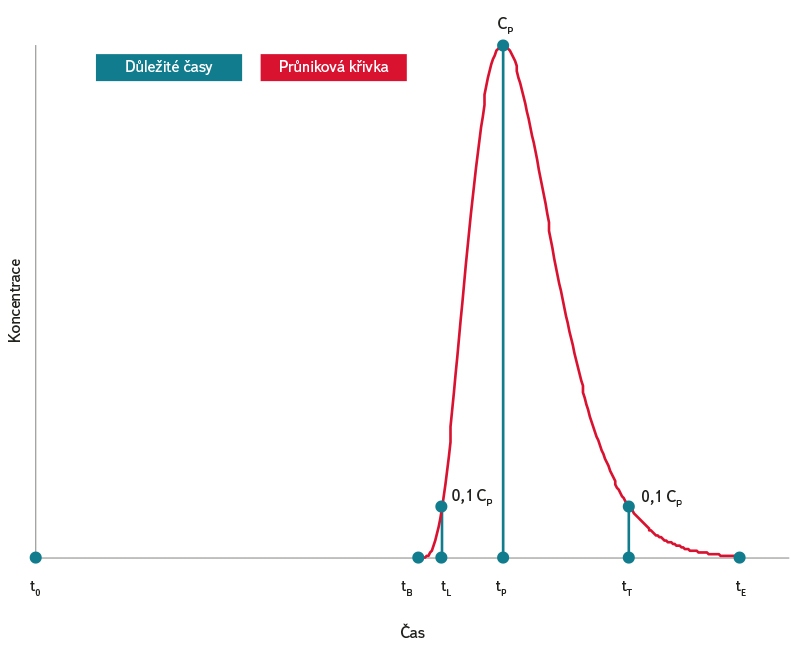
Obr. 1. Důležité dotokové doby
Fig. 1. Important travel times
Pro predikci maximální koncentrace v případě okamžitého vnosu je možno použít vzorec (1) uvedený v DBAM [3]:
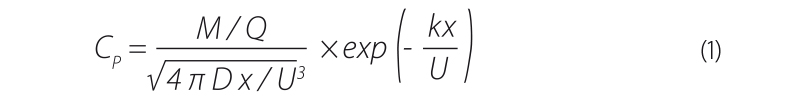
| kde | Cp | je | maximální koncentrace odpovídající vrcholu průnikové křivky ve vzdálenosti x od místa vnosu [g/m3], |
| M | hmotnost vnesené látky [g], | ||
| Q | průtok ve vzdálenosti x od místa vnosu [m3/s], | ||
| U | průřezová rychlost [m/s], | ||
| D | koeficient podélné disperze [m2/s], | ||
| k | rychlostní konstanta 1. řádu charakterizující objemové změny sledované látky [1/s], | ||
| t | čas [s], | ||
| x | vzdálenost zájmového od místa vnosu [m]. |
Další možností je použití empirického vzorce (2). Vychází ze vzorce, který uvádí Jobson [1] a je upraven pro nekonzervativní látku.
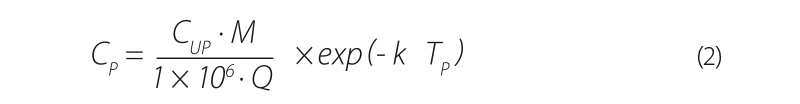
| kde | Cp | je | maximální koncentrace odpovídající vrcholu průnikové křivky ve vzdálenosti x od místa vnosu [g/m3], |
| M | hmotnost injektovaného stopovače [g], | ||
| Q | průtok ve vzdálenosti x od místa vnosu [m3/s], | ||
| Cup | maximální jednotková koncentrace ve vzdálenosti x od místa vnosu [1/s], | ||
| k | rychlostní konstanta 1. řádu charakterizující objemové změny sledované látky [1/hod]. |
Jednotková maximální koncentrace je definována jako 106 násobek maximální koncentrace při jednotkovém průtoku a jednotkové hmotnosti látky vnesené do toku [1]. Její závislost na dotokové době TP = tP – t0 může být vyjádřena empirickou rovnicí (3) uvedenou v [1]:

nebo rovnicí (4) rovněž uvedenou v [1]:
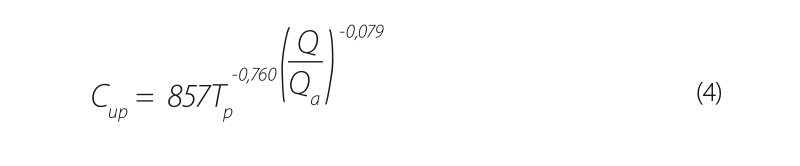
| kde | Tp = tP – t0 | je | dotoková doba odpovídající vrcholu průnikové křivky ve vzdálenosti x od místa vnosu [hod], |
| Q | průtok ve vzdálenosti x od místa vnosu [m3/s], | ||
| Qa | dlouhodobý průměrný průtok ve vzdálenosti x od místa vnosu [m3/s]. |
V empirických rovnicích (2), (3) a (4) se uvádějí dotokové doby v hodinách, proto rychlostní konstanta 1. řádu charakterizující objemové změny musí mít v rovnici (2) rozměr 1/hod.
V případě odhadu maximální koncentrace pro konzervativní látku je rychlostní konstanta 1. řádu charakterizující objemové změny sledované látky rovna nule. Pro bezpečný odhad maximální koncentrace při havarijním úniku nekonzervativní látky je nutno zvážit, zda není vhodné položit rychlostní konstantu 1. řádu charakterizující objemové změny rovněž rovnu nule.
Máme-li stanovenu maximální koncentraci Cp v zájmovém profilu ve vzdálenosti x od místa vnosu, je možno přistoupit k třetímu kroku, a tím je predikce rozdělení koncentrací během průchodu havarijního znečištění zájmovým profilem. V rámci přípravy modulu bylo hledáno takové rozdělení, které co nejvíce odpovídá skutečným hodnotám naměřeným v toku. Byla k tomu použita konkrétní data ze stopovacích pokusů na řece Svitavě [4].
Výsledky a diskuse
K predikci maximální koncentrace, kterou lze očekávat během průchodu havarijního znečištění zájmovým profilem, lze použít rovnici (1) nebo rovnici (2). Obě rovnice mají určité nevýhody. Nevýhodou rovnice (1) je obtížnost správného odhadu koeficientu podélné disperze. V odborné literatuře je totiž doporučeno mnoho různých postupů k určení tohoto koeficientu a výsledky jsou v některých případech značně rozdílné. Na nevýhody rovnice (2) upozorňuje ve své diplomové práci Kůrková [5]. Protože v rovnici (2) není zahrnuta podélná disperzivita, mohou se v grafech projevit její změny, především pokud byly zkoušky prováděny na různých místech a při různých průtocích.
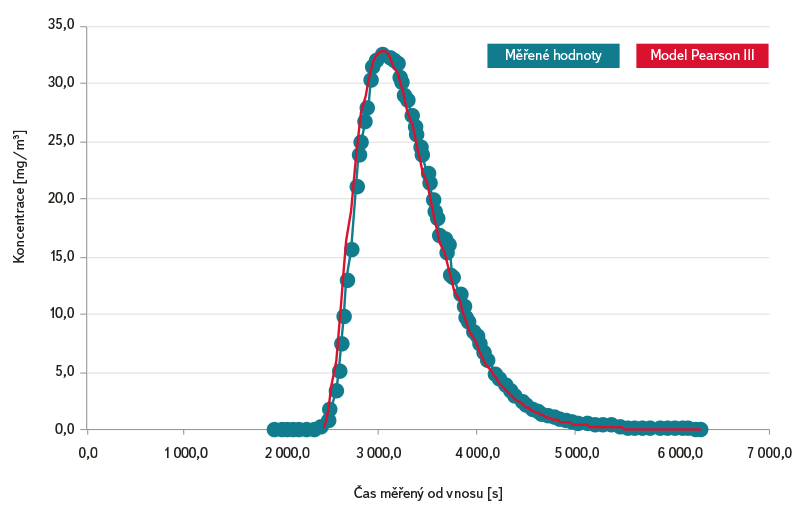
Obr. 2. Průniková křivka – Svitava PF1 – červen 2000
Fig. 2. Breakthroughcurve – Svitava PF1 – June 2000
Máme-li stanovenu maximální koncentraci Cp, v zájmovém profilu je možno přistoupit k třetímu kroku, a tím je predikce rozdělení koncentrací během průchodu havarijního znečištění zájmovým profilem. V povodí Odry nejsou v poslední době k dispozici žádné výsledky ze stopovacích pokusů, proto nezbylo, než se při přípravě modelu omezit na data získána odjinud. Různé varianty kroku tři byly ověřovány na konkrétních datech získaných stopovacími pokusy na řece Svitavě [4]. V práci [4] a v navazujících studiích byly průnikové křivky stopovače modelově aproximovány analytickým řešením, resp. za využití numerického modelu (MIKE11). V rámci přípravných studií projektu NAVAROSO byl proveden pokus provést aproximaci průnikové křivky stopovače pomocí Pearsonova rozdělení III. typu, které lze pro časy t > tB vyjádřit pomocí rovnice (5).
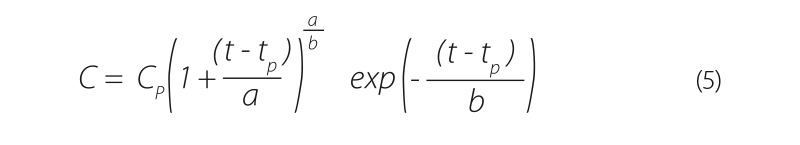
| kde | C | je | koncentrace v čase t [mg/m3], |
| Cp | koncentrace odpovídající vrcholu průnikové křivky [mg/m3], | ||
| t | čas [s], | ||
| tP | čas, ve kterém znečištění dosáhne maximální koncentrace v zájmovém profilu [s], | ||
| b | konstanta odpovídající době mezi tP a časem dosažení těžiště plochy pod průnikovou křivkou [s], | ||
| a | konstanta odpovídající době mezi tB a tP [s], | ||
| tB | čas příchodu nejrychlejších částic znečištění do zájmového profilu [s]. |
V časech t rovných nebo menších než tB předpokládáme, že profil nebude havarijním znečištěním ovlivněn. V případě, že se znečišťující látka vyskytuje v toku běžně i před havárií bude nutno rovnici (5) ještě upravit i pro tuto variantu. V případě, že znečišťující látka, která unikla při havárii je nekonzervativní, lze do rovnice (5) zavést ještě rychlostní konstantu objemových změn nebo rovnici zachovat v původním stavu ve prospěch bezpečnosti odhadu. Pro jednotlivé profily na řece Svitavě je na obr. 2 až 6 provedeno porovnání naměřených hodnot s modelem využívajícím Pearsonovo rozdělení III. typu. Vyvstává zde otázka, proč hledat zvláštní funkci pro aproximaci průnikových křivek (Pearson III), když funkční závislost za daných, výše uvedených předpokladů udává rovnice práce (1). Jedná se o snahu vyhnout se obtížnému stanovování koeficientu podélné disperze na základě proměnlivých parametrů říčního koryta. Podobnou snahu můžeme vidět například i u tvůrců modelu Riverspiell [6], když zavedli novou metodu využívající implicitní korelaci mezi koeficientem podélné disperze a dotokovou dobou. Snaha vyhnout se přímé závislosti na proměnlivých parametrech koryta toku (průtočná plocha, šířka, hloubka) je patrná i u rovnice (1).
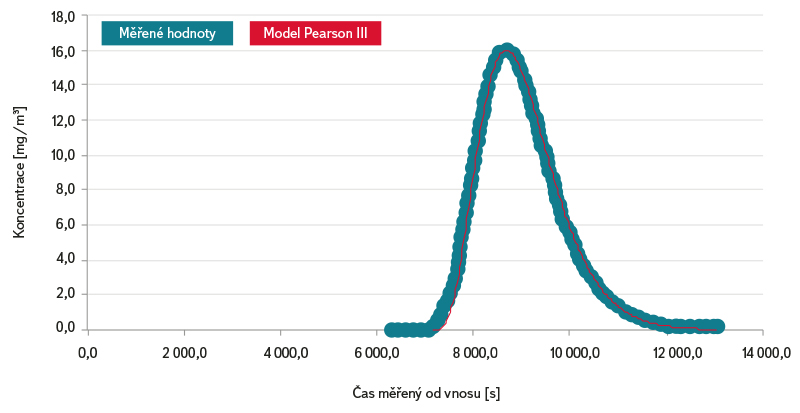
Obr. 3. Průniková křivka – Svitava PF2 – červen 2000
Fig. 3. Breakthroughcurve – Svitava PF2 – June 2000
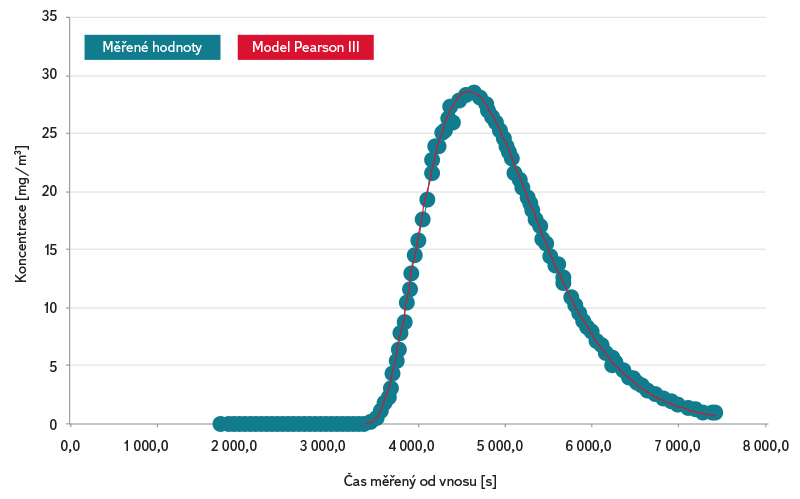
Obr. 4. Průniková křivka – Svitava PF1 – srpen 2000
Fig. 4. Breakthroughcurve – Svitava PF1 – August 2000
Výsledky jsou shrnuty v tabulce 1. Koeficienty a a b v rovnici (5) byly získány metodou pokus omyl. Young a kol. [7] doporučili pro posuzování těsnosti mezi predikovanými a měřenými hodnotami vzorec pro výpočet koeficientu determinace. Pro naše potřeby byl použit ve formě rovnice (6).

| kde | Rt | je | koeficient determinace [–], |
| Ci | i-tá hodnota měřené koncentrace [mg/m3], | ||
| CMi | i-tá hodnota koncentrace modelu [mg/m3], | ||
| p | počet měření v časech t > tB [–]. |
Autor Šajer [8] zjistil, že u všech pěti analyzovaných průnikových křivek lze vzestupnou část průnikové křivky vyjádřit pomocí rovnice (7).
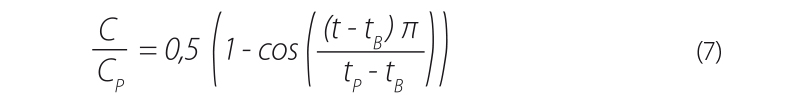
| kde | t | je | čas [s]. |
V praxi se při vyhodnocování stopovacích pokusů zjišťuje čas tL, pro který lze rovnici (7) upravit na rovnici (8).

Vezmeme-li v úvahu data, která uvádí Jobson v příloze [1], pak poměr mezi dobou potřebnou pro dosažení maximální koncentrace Cp v zájmovém profilu, tj. (tP – t0), a dobou od vnosu po příchod do zájmového profilu, při kterém je dosažena koncentrace jedna desetina maximální koncentrace Cp v zájmovém profilu, tj. (tL – t0), bývá blízko pod místem injektáže vyšší, s rostoucí vzdáleností se však většinou ustálí zhruba v rozmezí 1,1 : 1 až 1,3 : 1. Vyskytují-li se v toku významné oblasti s pomalým prouděním (tzv. mrtvé zóny), pak je nutno počítat s vyššími hodnotami. Jako příklad je možno uvést poměr 1,68 : 1, který byl zjištěn u řeky Punkvy [9]. Uvedené poměry se týkají okamžitého vnosu konzervativní látky do toku.
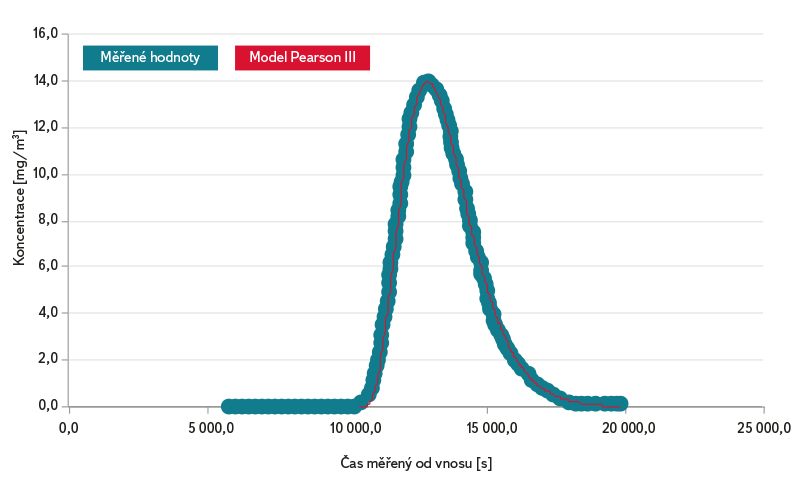
Obr. 5. Průniková křivka – Svitava PF2 – srpen 2000
Fig. 5. Breakthroughcurve – Svitava PF2 – August 2000
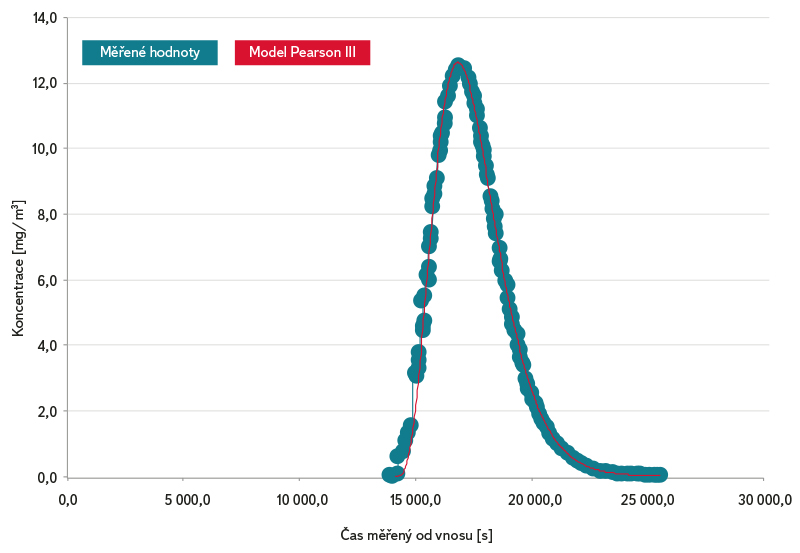
Obr. 6. Průniková křivka – Svitava PF21 – srpen 2000
Fig. 6. Breakthroughcurve – Svitava PF21 – August 2000
Na základě uvedených výsledků budou do připravovaného modelu v povodí řeky Odry vloženy vstupní hodnoty tzv. defaulty, které bude možno na základě dalších zkušeností pro jednotlivé toky postupně upravovat.
Rovnice (1) až (5) je možno použít pouze v případě okamžitého vnosu znečišťující látky do toku. V praxi se často vyskytuje při haváriích kontinuální vnos s omezenou dobou trvání. V tom případě lze při modelování koncentrace v zájmovém profilu vycházet z rozdělení pro okamžitý vnos (například z rovnice (5)) a následně použít metodu superpozice.
Závěr
Protože v poslední době nejsou v povodí Odry k dispozici žádná data ze stopovacích pokusů, byla pro přípravu modelu šíření znečištění v tomto povodí využita data ze stopovacích pokusů, které byly realizovány na Svitavě v roce 2000. Výsledné průnikové křivky se nejlépe podařilo popsat pomocí Pearsonova rozdělení 3. typu. Vychází se z analýzy pouze pěti průnikových křivek, pro zobecnění by bylo vhodné toto ověřit na dalších výsledcích z jiných stopovacích pokusů. Do připravovaného modulu v povodí Odry budou vloženy defaulty vycházející z výše uvedených poznatků, které bude možno na základě dalších zkušeností pro jednotlivé toky postupně upravovat.
Poděkování
Tento příspěvek vznikl díky podpoře projektu č. TH02030142 NAVAROSO, pro který je poskytovatelem podpory Technologická agentura České republiky.
