Proudění v oblouku Podkrušnohorského přivaděče

Souhrn

Článek se zabývá hydraulickým výzkumem proudění v oblasti oblouku v lokalitě Podkrušnohorského přivaděče (PKP IV – ř. km 2,812–2,736). Koryto přivaděče v oblouku je lichoběžníkového průřezu se sklonem stěn 9 : 1. Proudění je převážně bystřinného charakteru.

Obr. 1. Podkrušnohorský přivaděč
Fig. 1. Podkrušnohorský canal

Měření probíhala na fyzikálním modelu v měřítku 1 : 15, který byl postaven členy katedry hydrotechniky ve vodohospodářské laboratoři Fakulty stavební, ČVUT. Na fyzikálním modelu byly měřeny rychlosti a hladiny v celkem devíti profilech. Dále byl sestaven 3D matematický model v programu Ansys CFX, na kterém je možné kromě rychlostí a hladin pozorovat tvar proudového pole. Cílem výzkumu je vyhodnocení proudění v oblasti oblouku v režimu bystřinného proudění pomocí metod hybridního modelování a také verifikace matematického modelu pomocí hodnot naměřených na modelu.

Úvod

Přivaděč je soustava vodních kanálů, podzemních potrubí, nádrží a akvaduktu na Mostecku. Jeho výstavba probíhala v letech 1957–1982. Soustava se skládá z Přivaděče průmyslové vody a z Podkrušnohorského přivaděče. Účelem této 33,8 km dlouhé soustavy kanálu je ochrana před průnikem povrchových vod do hnědouhelných lomů Libouš, Šverma, Obránců míru a ČSA. Další funkcí je přivádět vodu z povodí řeky Ohře pro průmysl na Chomutovsku a Mostecku.

Zkoumaný oblouk se nachází v úseku PKP IV – ř. km 2,812–2,736, který se nachází u obce Vysoká Pec (obr. 1, 2). Úsek má lichoběžníkový profil se sklony stěn 9 : 1 a šířky ve dně 3,6 m, podélný sklon je 4,7 %, poloměr oblouku je 60 m. Jeho celková délka je necelých 80 m [1].

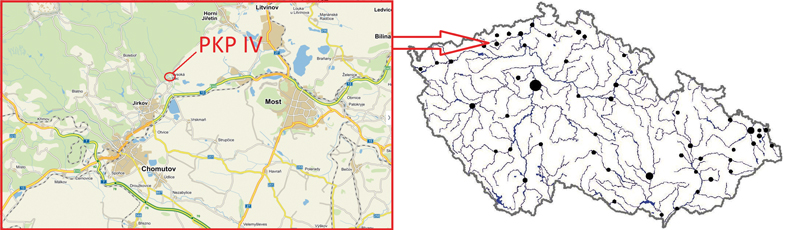
Obr. 2. Mapa PKP
Fig. 2. Map of PKP

Fyzikální model

Modelové podmínky

Model byl sestaven členy katedry hydrotechniky ve vodohospodářské laboratoři Fakulty stavební, ČVUT v rámci výzkumného projektu PPV a PKP – doplnění bezpečnostních prvků v korytě toku.

Pro fyzikální model bylo zvoleno měřítko 1 : 15 a přístup podle Froudova zákona podobnosti. U tohoto typu modelové podobnosti jsou vyjádřeny podmínky dynamické podobnosti hydrodynamických jevů za výhradního působení gravitačních sil.

Obr. 3. Fyzikální model PKP
Fig. 3. Physical Model of PKP

Kromě gravitačních sil však mohou zkoumané proudění ovlivňovat i další síly – odpor třením vazké kapaliny, síly kapilární, síly objemové apod. Podle Froudova zákona podobnosti můžeme určitý hydrodynamický jev zkoumat tehdy, jestliže účinky těchto sil jsou zanedbatelné v porovnání s gravitačními silami. Mezní podmínky vymezují oblasti a měřítka, v nichž lze hydrodynamický jev modelovat.

Kinematicky podobné jevy, které ovlivňuje výhradně gravitační síla, jsou dynamicky podobné, jestliže ve vzájemně příslušných průřezech budou stejná Froudova čísla. Fyzikální model v měřítku 1 : 15 odpovídá všem podmínkám [2, 3].

Na základě modelových podobností vyplývají pro použité geometrické měřítko 1 : 15 následující podmínky:

Geometrické měřítko:      M_h = M_l = M_b = 15    

Měřítko rychlostí:            M_v = M^1/2 _l = 3,87

Měřítko průtoků:             M_Q = M ^5/2 _l = 871,42

Měřítko časů:                 M_t = M^1/2 _l = 3,87

Popis modelu

Model, viz obr. 3, je tvořen uklidňovací a nátokovou nádrží, celkem 21 příčnými profily vymezujícími tvar modelu (10 profilů před objektem (vývarem) tvořící zatáčku, 6 profilů objektových a 5 profilů za objektem). V rámci této práce je pozornost zaměřena pouze na prvních 10 profilů před objektem vývaru.

Měřené veličiny

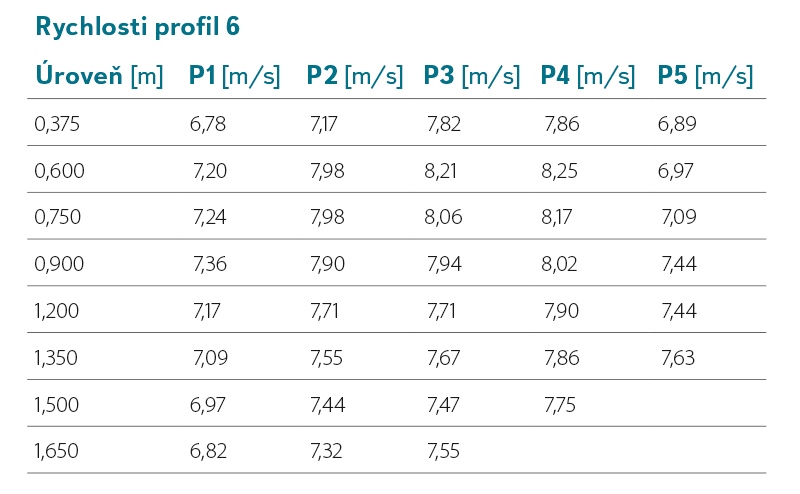
Rychlostní pole bylo měřeno pomocí dvou hydrometrických vrtulek typu STS 005 firmy Erfisinger electronic GmbH a dataloggeru. Získaná hodnota rychlosti je průměrná hodnota z 30 sekund měření. Měření probíhalo v každém profilu v 5 bodech v jednotlivých hloubkách. Rastr měření je vidět v tabulce 1. Celkem bylo měřeno 8 profilů, a to profil č. 3 až profil č. 10.

Tabulka 1. Měřené rychlosti – profil 6
Table 1. Measured velocity – profile 6

Měřené hloubky (obr. 4) byly převzaty z předešlých měření v rámci výzkumného projektu PPV a PKP – doplnění bezpečnostních prvků v korytě toku. Polohy hladin byly měřeny v každém profilu ve čtyřech bodech. Jako měřicí zařízení sloužily ultrazvukové sondy. Frekvence odečtu sond je 10 Hz a hodnoty hladin jsou následně získány jako průměr přes 10sekundový interval na každém profilu.

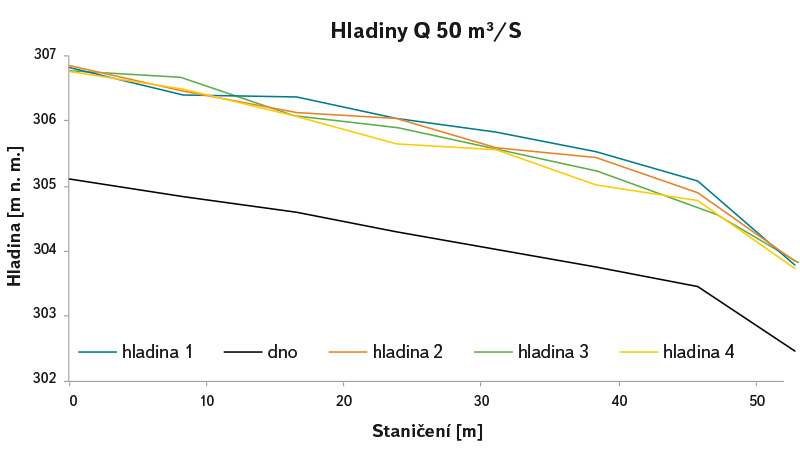
Obr. 4. Podélný profil
Fig. 4. Longitudinal profile

Měření probíhala v ustáleném režimu, kdy byla horní okrajová podmínka nastavena průtokem. Dolní okrajová podmínka byla tvořena nezatopeným výtokem. Rychlostní pole na modelu bylo měřeno celkem na šesti průtocích, a to 5, 10, 20, 30, 40 a 50 m³.s^-1.

Matematický model

V rámci výzkumu byl sestaven matematický model, který se skládá z nátokové nádrže a zkoumané části oblouku ukončené před vývarem (obr. 5).

Výpočetní síť byla vytvořena v programu ICEM CFD, který je součástí platformy ANSYS Workbench. Byla vytvořena strukturovaná síť (mesh) o maximální velikosti elementu 1 m. V místě oblouku byla síť zahuštěna na maximální velikost elementu 30 cm, aby nedocházelo ke zkreslení proudění v oblouku. Celkový počet elementů tak dosáhl 1 126 315.

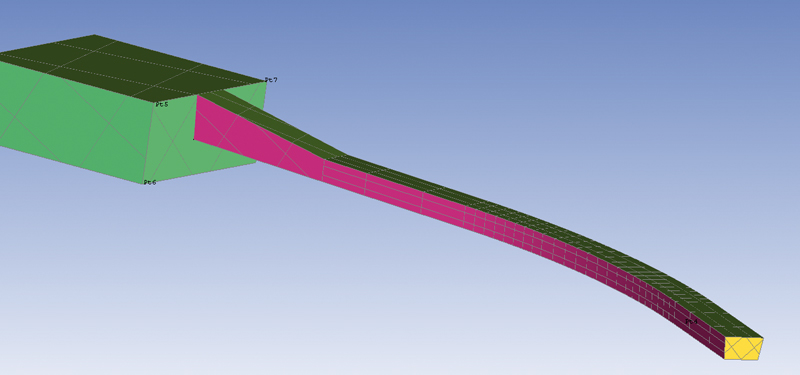
Obr. 5. Geometrie matematického modelu
Fig. 5. Geometry of the numerical model

Pro samotný výpočet byl použit program CFX, který je také součástí platformy ANSYS Workbench. Horní i dolní okrajová podmínka byla nastavena pomocí hladiny, které na fyzikálním modelu odpovídaly průtoku 50 m³.s^-1. Tento průtok pak sloužil pro kalibraci modelu. Kalibrace probíhala pomocí drsnosti stěn, kde počáteční hodnota drsnosti 0,014 byla měněna až na tzv. hladkou stěnu (no slip wall) [4, 5]. Model byl nastaven tak, aby umožňoval proudění s volnou hladinou (dvoufázové proudění voda­‑vzduch). Samotný výpočet je nastavený jako ustálené proudění.

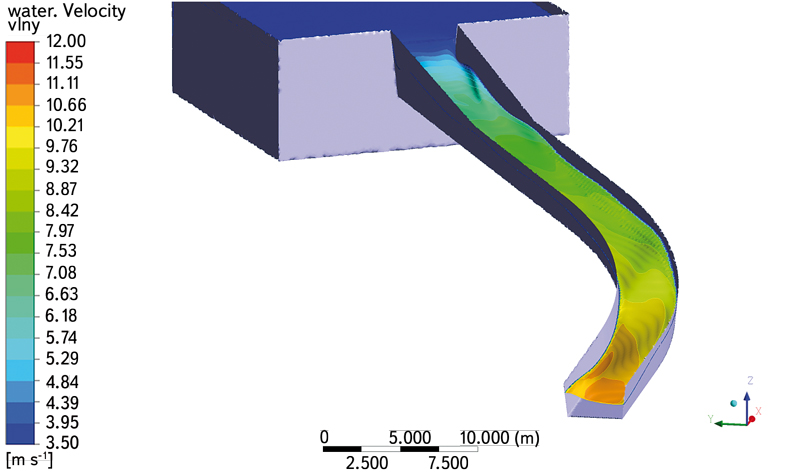
Obr. 6. Tvar hladiny z matematického modelu
Fig. 6. The shape of water level of the numerical model

Vyhodnocení

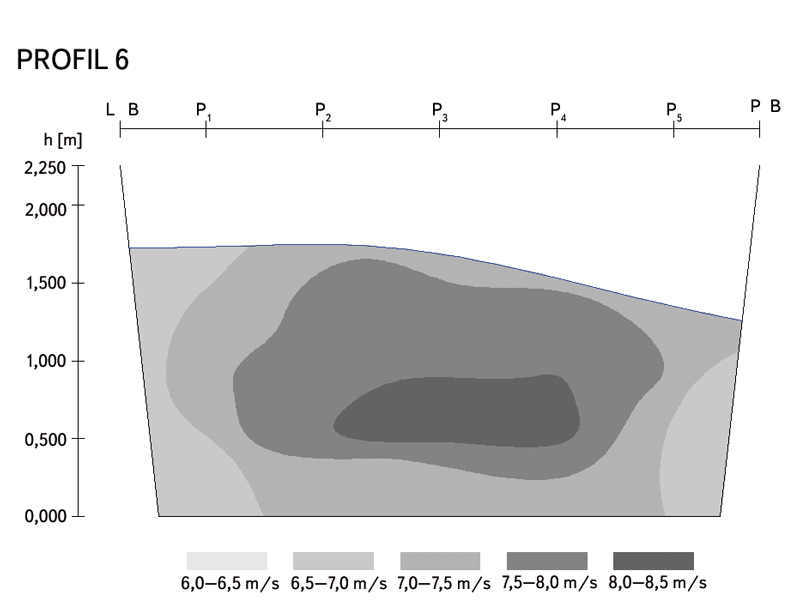
Rychlostní pole byla vyhodnocena pro návrhový maximální průtok 50 m³.s^-1. Rychlosti byly vykresleny pomocí plošné interpolace do jednotlivých profilů (obr. 6 a 7). Maximální rychlosti dosahovaly téměř 9 ms^-1. Rozložení rychlostí v jednotlivých profilech je plynulé, z toho lze vyvodit, že v celém oblouku nedochází k velkým turbulencím.

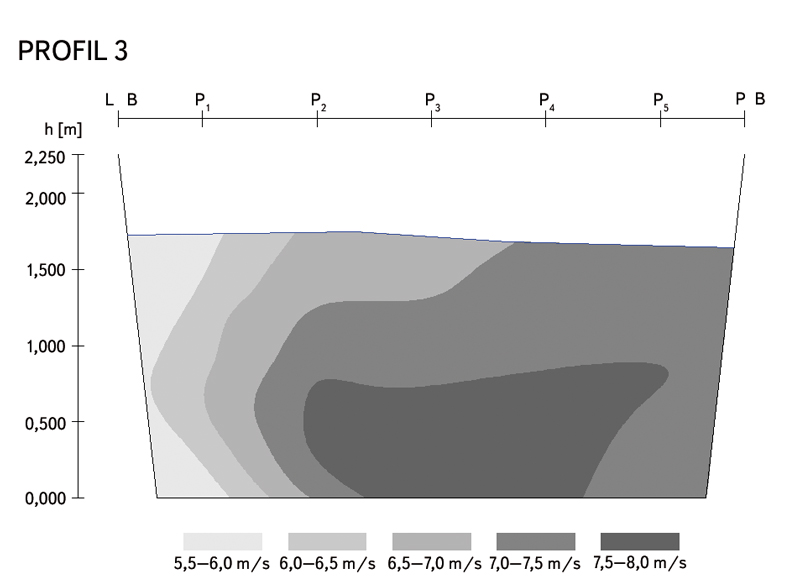
Obr. 7. Rychlosti profil 3
Fig. 7. The velocity profile 3

Obr. 8. Rychlosti profil 6
Fig. 8. The velocity profile 6

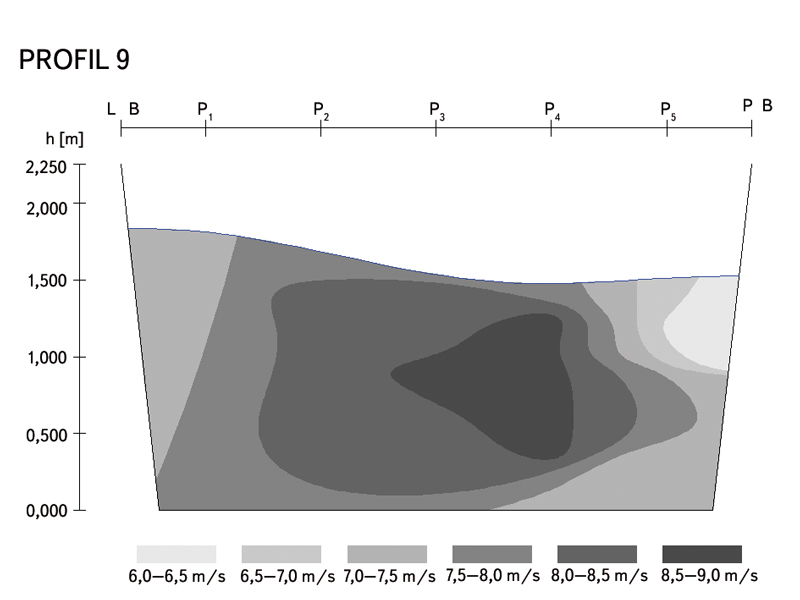
Obr. 9. Rychlosti profil 9
Fig. 9. The velocity profile 9

Matematický model umožnil popsat proudová pole. Na základě pozorování hladiny se očekávalo značně turbulentní proudění a šroubovitý tvar proudnic v druhé polovině oblouku. Oproti tomuto předpokladu se ukázalo, že proudnice jsou téměř plynulé a jsou plynulé v celé délce oblouku, viz obr. 8, 9 a 10.

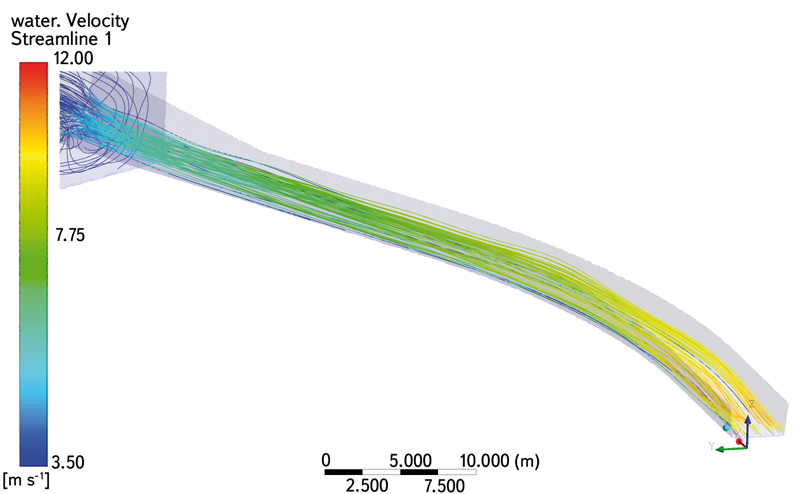
Obr. 10. Proudnice
Fig. 10. Streamline

Závěr

V rámci výzkumu bylo zkoumáno proudění v oblouku s velkým sklonem dna a bystřinným charakterem proudění. Metodou hybridního modelování bylo možné vyhodnotit nejen rychlosti v jednotlivých profilech, ale také proudová pole v tomto úseku, které bylo možno určit po úspěšné verifikaci matematického modelu z naměřeného průběhu hladin na fyzikálním modelu. Výzkum ukázal, že při vysokém sklonu dna i při velkých průtocích nedochází k turbulentnímu proudění v obloucích.

Poděkování

Tento příspěvek vznikl za podpory grantu SGS16/059/OHK1/1T/11 Výzkum hydraulicky komplikovaného proudění vody na hydrotechnických stavbách.