Souhrn
V článku popsaný model používá stochastickou předpověď různé délky. Předpověď je vždy kratší než 1 rok. Pro adaptivní řízení je použita pouze první hodnota řady řízených odtoků. Řada předpovězených přítoků vody do nádrže je transformována na řadu řízených odtoků vody z nádrže. Stochastické řízení pracuje s rozptylem řízených odtoků. Stochastické řízení pracuje s vějířem možných hodnot. Článek popisuje konstrukci a vyhodnocení adaptivního stochastického modelu, který používá pro optimalizaci evoluční algoritmy. Model byl použit pro stochastické řízení zásobní funkce nádrže. Při zadání vstupů (předpovězené hodnoty přítoků) je modelem pro zvolenou pravděpodobnost překročení vypočten řízený odtok vody z nádrže. Model byl testován i validován na umělé vodní nádrži (profil Bílovice nad Svitavou) z důvodu dostupnosti dat. Model řídil nádrž logicky a při zvýšení celkového počtu předpovědí (z 300 na 500) se zlepšil celkový průběh řízení. Další zvyšování celkového počtu předpovědí nepřineslo výrazné zlepšení. Model využívající evoluční algoritmy by potřeboval velké množství strojového času, a proto byly výpočty prováděny v clusteru.

Úvod
V současné době jsou v praxi používány při řízení zásobní funkce nádrže převážně deterministické modely. Výhodou použití deterministický modelů je pouze jeden výstup (hodnota) řídicí veličiny, avšak při používání pouze jedné hodnoty dochází díky silnému zjednodušení problematiky ke ztrátě přesnosti řízení či mylnému vyhodnocení situace (předpověď se může výrazněji odlišovat od skutečnosti, která byla předpokládána) [1]. Oproti tomu stochastické řízení pracuje s určitým rozptylem hodnot řídicích průtoků s daným pravděpodobnostním rozdělením, a proto dochází k výrazně lepší aproximaci skutečné problematiky řízení. Výhodou stochastického řízení je výběr možnosti řízení pro danou pravděpodobnost scénáře. Výběr pravděpodobností nám poskytne vějíř možností.
Pro stochastické řízení můžeme při adaptivním způsobu řízení využít metodu Monte Carlo [2]. Její využití v oblasti vodohospodářského řešení nádrží naráží na omezení z hlediska výpočetní techniky (velké nároky na strojový čas). Pro vyhodnocení opakovaných náhodných stavů je zapotřebí minimálně 300 opakování výpočtu. Adaptivní řízení s použitím metody Monte Carlo a využitím tradičních algoritmů pro optimalizaci (kritériem optimalizace budeme v textu chápat odchylku mezi nadlepšeným a řízeným odtokem, která bude minimalizována) je vhodnou volbou pro stochastické řízení. Avšak výpočetní doba je pro běžné počítače neúnosná. Velké požadavky na výpočetní techniku jsou způsobeny především optimalizací, která je použita v každém časovém kroku, ve kterém opakovaně korigujeme řízení (vychází z principu adaptivity). Optimalizace využívá tradiční algoritmy (Diferenciální evoluci). Výpočty byly prováděny v clusteru, protože nároky na strojový čas u běžného počítače by byly neúnosné. Cílem je navrhnout algoritmus, který bude účinně minimalizovat ekonomické ztráty vzniklé z nedodávky vody (nesplněné hodnoty odtoku vody). Mělčí avšak delší poruchy (např. mírné omezení výroby) jsou ekonomicky výrazně příznivější než hlubší a kratší poruchy (např. výrazné omezení, zastavení výroby, nedostatečný průtok vody v toku pro směsný poměr s vodou vypouštěnou z čistírny odpadních vod atd.) Pro sestavení a práci s modelem byl použit program Matlab 2013.
Model
Model používá princip adaptivity a jeho jádrem je optimalizační modul využívající diferenciální evoluci (DE) [3], která používá tři rodiče. Modelu je poskytnuta řada budoucích přítoků vody do nádrže (předpovězené průtoky), na základě kterých by měl být model schopen najít nejlepší možné řešení podle kriteriální funkce, pokud by přítoky vody do nádrže nebyly zatíženy nejistotami. Nejistota spojená s předpovědí může vést k jinému průběhu řízení, než které by poskytla 100% předpověď (reálná řada) [4].
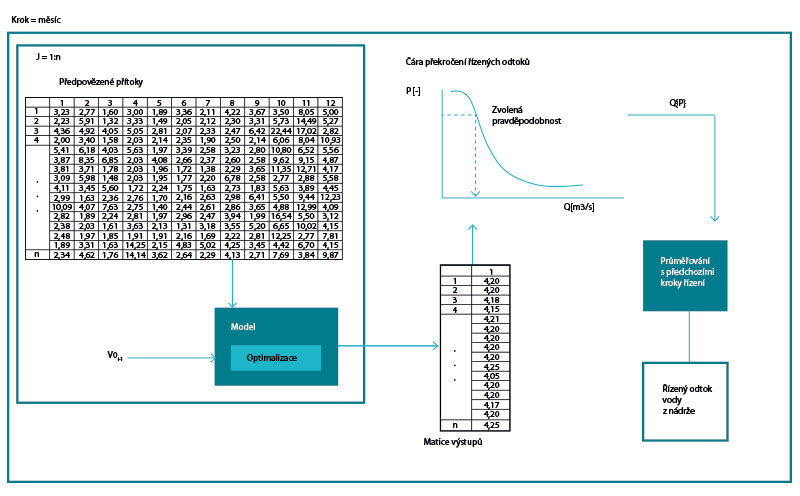
Obr. 1. Řídicí algoritmus modelu
Fig. 1. Control algorithm of model
Uvedená nejistota může způsobit rychlejší průběh prázdnění zásobního objemu vody nádrže, než jak by bylo potřebné (nádrž je prázdněna po skocích, ne plynule). Rychlost (gradient) prázdnění nádrže je hlídána modelem, a pokud rychlost prázdnění nabývá výrazných hodnot ve dvou časových úsecích po sobě jdoucích, model odtok vody z nádrže sníží o poměr mezi rychlostí prázdnění a maximální hodnotou zásobního objemu pro následující časový krok. Druhým důvodem zavedení pomocného algoritmu je, že metoda DE pracuje s celým zásobním objemem nádrže (včetně předpovědi). Pokud bude předpověď vyšší než reálný průtok, který nastane, může se při dlouho trvajícím suchu vyčerpat velmi rychle po skocích celý zásobní prostor nádrže a následně dojde ke vzniku velmi hluboké poruchy. Poruchy při řízení dodávky vody by měly být ideálně mělčí a delší než kratší a hlubší. Model provede řízení pro všechny předpovědi, sestaví empirickou čáru překročení řízených odtoků a odečte odtok vody z nádrže pro požadovanou pravděpodobnost. Poté je hodnota odtoku korigována a podle rovnice (1) je spočtena nová hodnota zásobního objemu. Kriteriální funkce je suma druhých mocnin odchylek řízeného odtoku vody z nádrže od řídícího odtoku vody z nádrže. Na obr. 1 je uveden hlavní algoritmus řízení nádrže.

| Kde | Qi [m3/s] | je | vypočtený odtok vody pro zvolenou pravděpodobnost, |
| Qpi [m3/s] | reálný přítok vody do nádrže, | ||
| Vi [m3/s] | objem vody v nádrži na počátku řešeného kroku, | ||
| Vi+1 [m3/s] | na konci řešeného kroku. |
Korekce řízení
Při použití metody DE jsou řízené odtoky vody často velmi rozkolísané, a proto bylo přistoupeno ke korekci řízeného odtoku vody. Korekce vychází z myšlenky metody konjugovaných gradientů. Řízený odtok vody z nádrže je zprůměrován s předchozími kroky řízení pro danou pravděpodobnost řízeného odtoku vody z nádrže.
Aplikace
Model byl aplikován na fiktivní nádrž na řece Svitavě (obr. 2, měrný profil Bílovice nad Svitavou). Místo aplikace bylo vybráno pro dostupnost dat. Nádrž byla navržena tak, aby došlo k výrazným poruchám během trénovacího období (délka 15 let). Nádrž byla řízena adaptivně s časovým krokem jeden měsíc. Řídicí odtok byl nastaven na hodnotu 4,25 m3/s a maximální objem vody v nádrži byl stanoven na 19,76 m3/s (objem je uveden v poměrných jednotkách jako podíl objemu za jednotku času, pokud by z nádrže byla vypouštěna hodnota poměrného objemu po dobu 1 průměrného měsíce = 2 630 000 s, byl by celý zásobní objem nádrže vyprázdněn). Maximální objem vody v nádrži a řídicí odtok byly zvoleny tak, aby docházelo v testovacím období k výrazným poruchám (nedodávce vody). Model provedl řízení s pravděpodobností odtoku 99, 95, a5, 5, 0,01 % pro délky předpovědí 1 až 12 měsíců. Předpovědi průměrných měsíčních přítoků byly získány z modifikovaného zonálního lineárního autoregresivního rekurentního modelu [5].
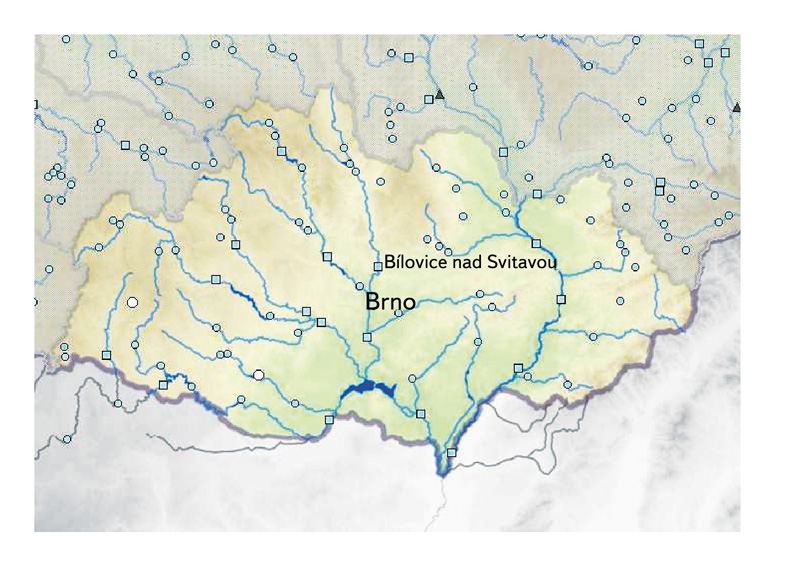
Obr. 2. Měrný profil Bílovice nad Svitavou
Fig. 2. Measured profile Bílovice nad Svitavou
Vyhodnocení
Hlavním kritériem úspěšnosti řízení byla druhá mocnina chyby mezi výstupy z modelu používající předpovězené přítoky a řízením, které bylo získáno z klasického modelu za použití 100% předpovědi (reálná průtoková řada) [6]. Počet zpětně uvažovaných kroků silně ovlivňoval průběh řízení a pravděpodobnost, pro kterou byly dosaženy nejlepší výsledky (obr. 3). Za nejlepší průběh řízení bylo považováno nejvyrovnanější řízení s mělkými poruchami. Uvedené obrázky grafů mají totožné osy, kdy na svislé ose je vždy řízený odtok vody z nádrže pro vybranou pravděpodobnost odtoku vody z nádrže a na vodorovné ose je čas v měsících. V legendě číslo uvedené za P (pravděpodobnost) značí uvažovanou pravděpodobnost řízeného odtoku vody z nádrže.
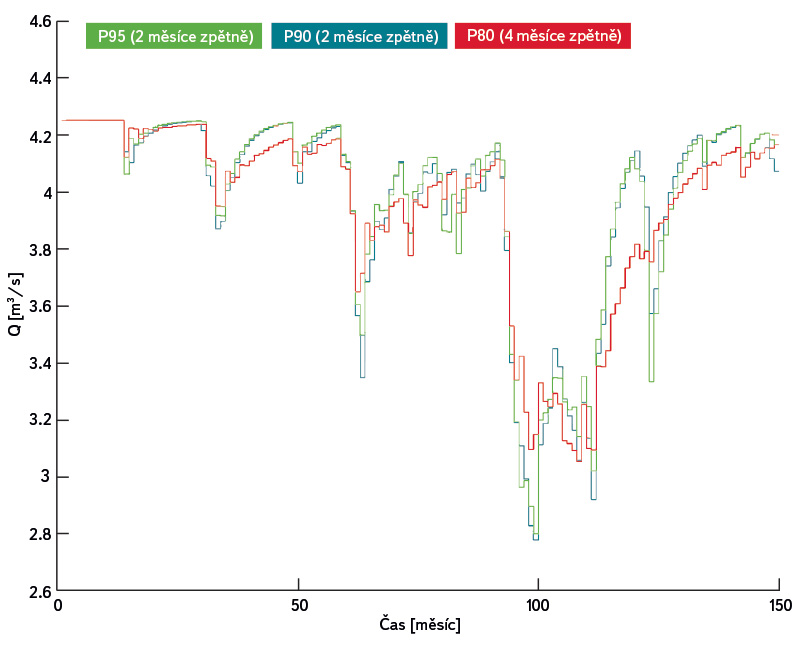
Obr. 3. Výsledky pro různý počet předchozích kroků řízení použitých pro průměrování
Fig. 3. Result for different numbers of backward steps of management used for averaging
Druhým významným faktorem, který ovlivní celkový průběh řízení, je délka předpovědi. Z výsledků bylo zjištěno (obr. 4), že nejlepších výsledků bylo dosaženo při délce předpovědi šest měsíců a použití čtyř kroků řízení zpětně pro průměrování. Při použití kratší délky předpovědi než šest měsíců je velmi zmenšen počet pravděpodobností, pro které nedojde k úplnému vyčerpání zásobního objemu (P99, P95), a umělé poruchy jsou hlubší než pro delší předpověď. Použití delší předpovědi než šest měsíců nepřineslo výrazné zlepšení. Výsledky pro délku předpovědi osmi a šesti měsíců jsou téměř totožné, uvedené tvrzení neplatí pro potřebnou délku výpočty.
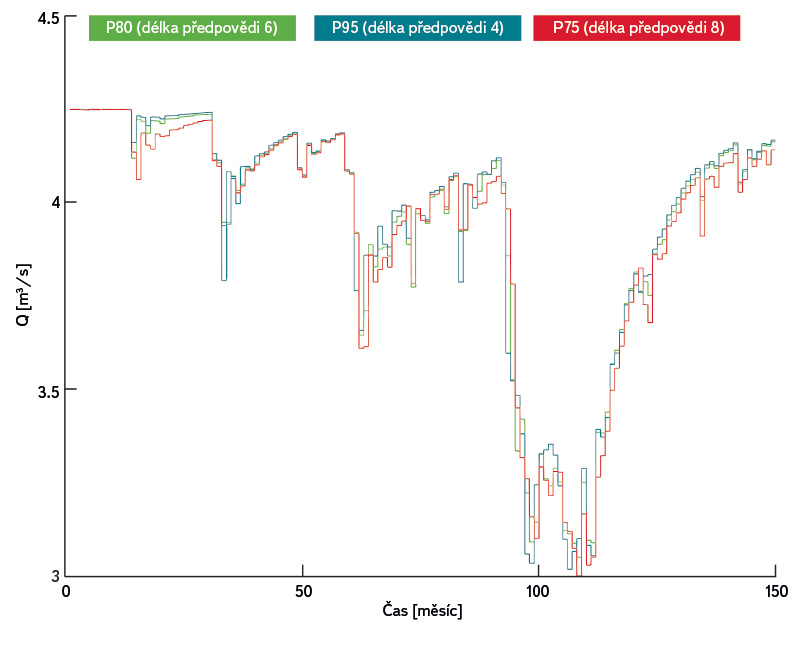
Obr. 4. Vliv délky předpovědi na průběh řízení
Fig. 4. Influnce lenght of forecast on course of management
Během řízeného období model vytvářel umělé poruchy, avšak průběh řízení byl velmi dobrý i při srovnání s klasickým modelem (100% předpověď) (obr. 5).
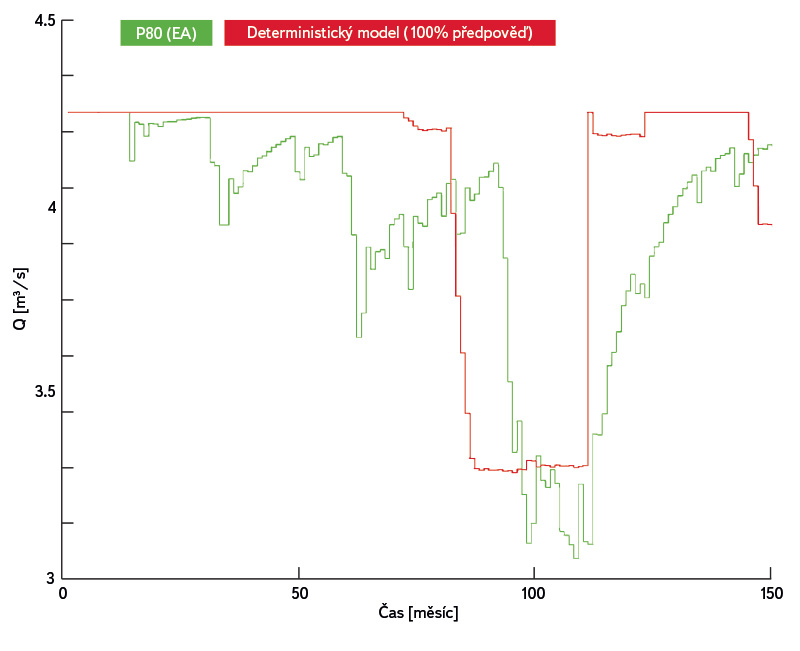
Obr. 5. Porovnání stochastického modelu a deterministického modelu
Fig. 5. Comparison between results of stochastic model and results of deterministic model
Závěr
Z výše uvedeného textu vyplývá, že výsledné řízení je závislé na požadované pravděpodobnosti, s níž by se měly přítoky vyskytnout a s nimi i požadovaný odtok vody z nádrže. Nelze opomenout, že výsledné řízení je závislé na celkovém počtu i délce předpovědí a počtu kroků uvažovaných při řízení zpětně. Při vyšším počtu předpovědí dochází ke zlepšení řízení. Vyhodnocení stochastického řízení vyžadovalo velké množství strojového času a výpočty na clusterech. Srovnatelný výpočet (150 měsíců, délka předpovědi 8 a počet předpovědí 500, 10 pravděpodobností) trval na clusteru 10 hodin, na běžném stolním PC bylo potřeba 7 dní. Výsledky ukazují, že lze zásobní funkci nádrže řídit stochasticky pomocí metody DE a stochastického modifikovaného zonálního předpovědního modelu.
Poděkování
Článek vznikl za podpory projektu Řízení zásobní funkce nádrží při uvažování nejistot hydrologických vstupů s použitím metod umělé inteligence s podporou stochastických předpovědních modelů.
